[题目]已知函数f(x)=﹣x2+bln上单调递减.则b的取值范围( )A.[0.+∞)B.[﹣ .+∞)C.(﹣∞.0]D.(﹣∞.﹣ ] 题目和参考答案——青夏教育精英家教网—

【题目】已知函数f（x）=﹣x2+bln（x+1）在[0，+∞）上单调递减，则b的取值范围（）
A.[0，+∞）
B.[﹣ ，+∞）
C.（﹣∞，0]
D.（﹣∞，﹣ ]

【答案】C
【解析】解：由题意知函数f（x）=﹣x2+bln（x+1）的定义域为（﹣1，+∞）；
则f'（x）=﹣2x+ ；
f（x）在[0，+∞）上单调递减，则f'（x）在[0，+∞）上恒有f'（x）≤0；
所以：﹣2x+ ≤0b≤2x（x+1）
令g（x）=2x（x+1），则g（x）在[0，+∞）上的最小值为g（0）=0：
所以b的取值范围为：（﹣∞，0]
故选：C
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系：在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减才能正确解答此题．

练习册系列答案

赢在起跑线快乐寒假河北少年儿童出版社系列答案

天利38套中考总复习命题规律与必考压轴题系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某高中社团进行社会实践，对岁的人群随机抽取n人进行了一次是否开通“微博”的调查，若开通“微博”的称为“时尚族”，否则称为“非时尚族”，通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图：

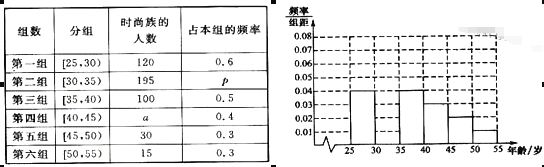
完成以下问题：

（Ⅰ）补全频率分布直方图并求的值；

（Ⅱ）从岁年龄段的“时尚族”中采用分层抽样法抽取人参加网络时尚达人大赛，其中选取人作为领队，记选取的名领队中年龄在岁的人数为，求的分布列

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】先阅读下列题目的证法，再解决后面的问题．

已知a1，a2∈R，且a1＋a2＝1，求证：a＋a≥.

证明：构造函数f(x)＝(x－a1)2＋(x－a2)2，则f(x)＝2x2－2(a1＋a2)x＋a＋a＝2x2－2x＋a＋a.

因为对一切x∈R，恒有f(x)≥0，

所以Δ＝4－8(a＋a)≤0，从而得a＋a≥.

(1)若a1，a2，…，an∈R，a1＋a2＋…＋an＝1，请由上述结论写出关于a1，a2，…，an的推广式；

(2)参考上述证法，请对你推广的结论加以证明．

查看答案和解析>>

科目：高中数学 来源： 题型：

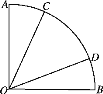
【题目】如图所示，在圆心角为90°的扇形AOB中，以圆心O作为起点作射线OC，OD，则使∠AOC＋∠BOD＜45°的概率为(　　)

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某大学为调查来自南方和北方的同龄大学生的身高差异，从2016级的年龄在18～19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名，测量他们的身高，量出的身高如下(单位：cm)：

南方：158，170，166，169，180，175，171，176，162，163.

北方：183，173，169，163，179，171，157，175，184，166.

(1)根据抽测结果，画出茎叶图，对来自南方和北方的大学生的身高作比较，写出统计结论．

(2)设抽测的10名南方大学生的平均身高为x cm，将10名南方大学生的身高依次输入如图所示的程序框图进行运算，问输出的s大小为多少？并说明s的统计学意义．

(3)为进一步调查身高与生活习惯的关系，现从来自南方的这10名大学生中随机抽取2名身高不低于170 cm的学生，求身高为176 cm的学生被抽中的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数y=f（x﹣1）的图象关于点（1，0）对称，且当x∈（﹣∞，0），f（x）+xf′（x）＜0成立．若a=（20.2）f（20.2），b=（ln2）f（ln2），c=（log2 ）f（log2 ），则a，b，c的大小关系是（）
A.a＞b＞c
B.b＞a＞c
C.c＞a＞b
D.a＞c＞b