
分析 三棱锥O-EFG的高为圆柱的高,即高为ABC,当三棱锥O-EFG体积取最大值时,△EFG的面积最大,当EF为直径,且G在EF的垂直平分线上时,(S△EFG)max=$\frac{1}{2}×4×2=4$,由此能求出三棱锥O-EFG体积的最大值.
解答 解: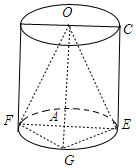 ∵将矩形ABCD绕边AB旋转一周得到一个圆柱,AB=3,BC=2,
∵将矩形ABCD绕边AB旋转一周得到一个圆柱,AB=3,BC=2,
圆柱上底面圆心为O,△EFG为下底面圆的一个内接直角三角形,
∴三棱锥O-EFG的高为圆柱的高,即高为ABC,
∴当三棱锥O-EFG体积取最大值时,△EFG的面积最大,
当EF为直径,且G在EF的垂直平分线上时,
(S△EFG)max=$\frac{1}{2}×4×2=4$,
∴三棱锥O-EFG体积的最大值Vmax=$\frac{1}{3}×({S}_{△EFG})_{max}×AB$=$\frac{1}{3}×4×3=4$.
故答案为:4.
点评 本题考查三棱锥的体积的最大值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
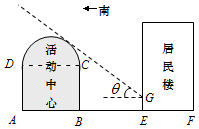 如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE=30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足$tanθ=\frac{3}{4}$.
如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE=30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足$tanθ=\frac{3}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com