
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当m>0时,若对于区间[1,2]上的任意两个实数x1,x2,且x1<x2,都有![]() ,成立,求m的最大值.
,成立,求m的最大值.
【答案】(1)见解析 (2)![]() .
.
【解析】
(1)先求导,再分类讨论,根据导数和函数的单调性的关系即可解决,(2)根据题意可得f(x2)-x22)<f(x1)-x12,构造函数,再求导,再分离参数,利用导数求出函数的最值即可.
(1)f(x)的定义域是(0,+∞), f′(x)=x+m+![]() =
=![]() ,
,
m≥0时,f′(x)>0, 故m≥0时,f(x)在(0,+∞)递增;
m<0时,方程x2+mx+m=0的判别式为: △=m2-4m>0,
令f′(x)>0,解得:x>![]() ,
,
令f′(x)<0,解得:0<x<![]() ,
,
故m<0时,f(x)在(![]() ,+∞)递增,在(0,
,+∞)递增,在(0,![]() )递减;
)递减;
(2)由(1)知,当m>0时,函数f(x)在(0,+∞)递增,
又[1,2]![]() (0,+∞),故f(x)在[1,2]递增;
(0,+∞),故f(x)在[1,2]递增;
对任意x1<x2,都有f(x1)<f(x2), 故f(x2)-f(x1)>0,
由题意得:f(x2)-f(x1)<![]() , 整理得:f(x2)-
, 整理得:f(x2)-![]() <f(x1)-
<f(x1)-![]() ,
,
令F(x)=f(x)-x2=-![]() x2+mx+mlnx, 则F(x)在[1,2]递减, 故F′(x)=
x2+mx+mlnx, 则F(x)在[1,2]递减, 故F′(x)=![]() ,
,
当x∈[1,2]时,-x2+mx+m≤0恒成立,即m≤![]() ,
,
令h(x)=![]() ,则h′(x)
,则h′(x)![]() >0, 故h(x)在[1,2]递增,
>0, 故h(x)在[1,2]递增,
故h(x)∈[![]() ,
,![]() ], 故m≤
], 故m≤![]() .
.
![]() 实数
实数![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln2x-2aln(ex)+3,x∈[e-1,e2]
(1)当a=1时,求函数f(x)的值域;
(2)若f(x)≤-alnx+4恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知函数![]() ,其中
,其中![]() ,求函数
,求函数![]() 的图象恰好经过第一、二、三象限的概率;
的图象恰好经过第一、二、三象限的概率;
(2)某校早上8:10开始上课,假设该校学生小张与小王在早上7:30~8:00之间到校,且每人到该时间段内到校时刻是等可能的,求两人到校时刻相差10分钟以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若平面直角坐标系内两点P,Q满足条件:①P,Q都在函数f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数f(x)的图象上的一个“友好点对”(点对(P,Q)与点对(Q,P)看作同一个“友好点对”).已知函数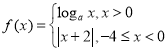
![]() ,若此函数的“友好点对”有且只有一对,则实数
,若此函数的“友好点对”有且只有一对,则实数![]() 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 的元素个数为
的元素个数为![]() 个且元素为正整数,将集合
个且元素为正整数,将集合![]() 分成元素个数相同且两两没有公共元素的三个集合
分成元素个数相同且两两没有公共元素的三个集合![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,若集合
,若集合![]() 中的元素满足
中的元素满足![]() ,
,![]() ,
,![]() ,则称集合
,则称集合![]() 为“完美集合”例如:“完美集合”
为“完美集合”例如:“完美集合”![]() ,此时
,此时![]() .若集合
.若集合![]() ,为“完美集合”,则
,为“完美集合”,则![]() 的所有可能取值之和为( )
的所有可能取值之和为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 过点
过点![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设![]() ,
,![]() 是过点
是过点![]() 且关于直线
且关于直线![]() 对称的两条直线,
对称的两条直线,![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点. 求证:
两点. 求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com