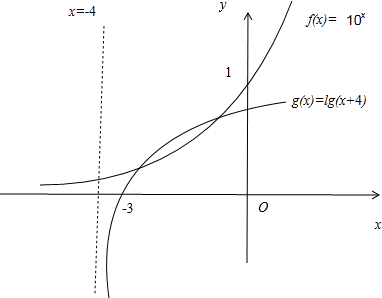
分析:作出函数g(x)=lg(x+4)与函f(x)=10x的图象,结合函数的图象可判断两函数的交点的个数及交点所在的区间,从而可判断 方程的根的存在情况
解答:解:作出函数g(x)=lg(x+4)与函f(x)=10
x的图象
∵函数f(x),g(x)在(-4,+∞)都单调递增,但是从函数增加的速度上看,函数g(x)比着f(x)的增加速度先快后慢
令F(x)=lg(x+4)-10
x,x>-4,则
F(x)=-∞<0
∵F(-2)=lg(2)-10
-2>0,F(0)=lg(4)-10
0<0,
∴F(x)=0在(-4,-2)上有一根,在(-2,0)上有一根
当x>0时,10
x比lg(x+4)增加的速度快,不再有交点了
∴函数f(x)与g(x))的图象只有2个交点
即方程lg(x+4)=10
x有2个负根
故选:C
点评:本题主要考查了结合函数的图象判断方程的根的个数及根的存在区间,解题的关键是由f(0)>g(0)可知两交点都在(-3,0),容易出现把第二个根当成正数的错误.



