
ΓΨΧβΡΩΓΩΝΫœΊ≥«![]() ΚΆ
ΚΆ![]() œύΨύ
œύΨύ![]() Θ§œ÷ΦΤΜ°‘ΎΝΫœΊ≥«ΆβΈΜ”ΎœΏΕΈ
Θ§œ÷ΦΤΜ°‘ΎΝΫœΊ≥«ΆβΈΜ”ΎœΏΕΈ![]() …œ―Γ‘ώ“ΜΒψ
…œ―Γ‘ώ“ΜΒψ![]() Ϋ®‘λ“ΜΗωΝΫœΊ≥«ΒΡΙΪΙ≤ά§Μχ¥Πάμ≥ßΘ§“―÷Σά§Μχ¥Πάμ≥ßΕ‘≥« –ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥« –ΒΡΒΡΨύάκΙΊœΒΉν¥σΘ§ΤδΥϊ“ρΥΊ”ΑœλΫœ–Γ‘ί ±≤ΜΩΦ¬«Θ§ά§Μχ¥Πάμ≥ßΕ‘≥«
Ϋ®‘λ“ΜΗωΝΫœΊ≥«ΒΡΙΪΙ≤ά§Μχ¥Πάμ≥ßΘ§“―÷Σά§Μχ¥Πάμ≥ßΕ‘≥« –ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥« –ΒΡΒΡΨύάκΙΊœΒΉν¥σΘ§ΤδΥϊ“ρΥΊ”ΑœλΫœ–Γ‘ί ±≤ΜΩΦ¬«Θ§ά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»ΈΣΕ‘≥«
ΒΡΉή”ΑœλΕ»ΈΣΕ‘≥«![]() ”κ≥«
”κ≥«![]() ΒΡ”ΑœλΕ»÷°ΚΆ. Φ«
ΒΡ”ΑœλΕ»÷°ΚΆ. Φ«![]() ΒψΒΫ≥«
ΒψΒΫ≥«![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() Θ§Ϋ®‘Ύ
Θ§Ϋ®‘Ύ![]() ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«
¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»ΈΣ
ΒΡΉή”ΑœλΕ»ΈΣ![]() Θ§Ά≥ΦΤΒς≤ι±μΟςΘΚά§Μχ¥Πάμ≥ßΕ‘≥«
Θ§Ά≥ΦΤΒς≤ι±μΟςΘΚά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥«
ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥«![]() ΒΡΨύάκΒΡΤΫΖΫ≥…Ζ¥±»Θ§±»άΐœΒ ΐ2.7ΘΜά§Μχ¥Πάμ≥ßΕ‘≥«
ΒΡΨύάκΒΡΤΫΖΫ≥…Ζ¥±»Θ§±»άΐœΒ ΐ2.7ΘΜά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥«
ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥«![]() ΒΡΨύάκΒΡΤΫΖΫ≥…Ζ¥±»Θ§±»άΐœΒ ΐΈΣ
ΒΡΨύάκΒΡΤΫΖΫ≥…Ζ¥±»Θ§±»άΐœΒ ΐΈΣ![]() ΘΜ«“Β±ά§Μχ¥Πάμ≥ß
ΘΜ«“Β±ά§Μχ¥Πάμ≥ß![]() ”κ≥«
”κ≥«![]() ΨύάκΈΣ
ΨύάκΈΣ![]() ±Ε‘≥«
±Ε‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»ΈΣ0.029.
ΒΡΉή”ΑœλΕ»ΈΣ0.029.
(1) ΫΪ![]() ±μ Ψ≥…
±μ Ψ≥…![]() ΒΡΚ· ΐΘΜ
ΒΡΚ· ΐΘΜ
(2) Χ÷¬έΔ≈÷–Κ· ΐΒΡΒΞΒς–‘Θ§≤Δ≈–Εœ‘ΎœΏΕΈ![]() …œ «Ζώ¥φ‘Ύ“ΜΒψΘ§ ΙΫ®‘Ύ¥Υ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«
…œ «Ζώ¥φ‘Ύ“ΜΒψΘ§ ΙΫ®‘Ύ¥Υ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»Ήν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΗΟΒψΒΫ≥«
ΒΡΉή”ΑœλΕ»Ήν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΗΟΒψΒΫ≥«![]() ΒΡΨύάκΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΒΡΨύάκΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©Κ· ΐ‘Ύ
ΘΜΘ®2Θ©Κ· ΐ‘Ύ![]() ΡΎΒΞΒςΒίΦθΘ§‘Ύ
ΡΎΒΞΒςΒίΦθΘ§‘Ύ![]() ΡΎΒΞΒςΒί‘ωΘΜ‘ΎœΏΕΈAB…œ¥φ‘Ύ
ΡΎΒΞΒςΒί‘ωΘΜ‘ΎœΏΕΈAB…œ¥φ‘Ύ![]() ΒψΖϊΚœΧβ“βΘ§ΗΟΒψ”κ≥«
ΒψΖϊΚœΧβ“βΘ§ΗΟΒψ”κ≥«![]() ΒΡΨύάκ
ΒΡΨύάκ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»«σ≥ωά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΒΡ”ΑœλΕ»±»άΐœΒ ΐ
ΒΡ”ΑœλΕ»±»άΐœΒ ΐ![]() Θ§»ΜΚσΗυΨίΧβ“β«σ
Θ§»ΜΚσΗυΨίΧβ“β«σ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒΘΜ
ΒΡΚ· ΐΙΊœΒΘΜ
Θ®2Θ©”Π”ΟΒΦ ΐ«σΫβ.
Δ≈ΨίΧβ“βΘ§![]() Θ§
Θ§![]() Θ§
Θ§
![]()
«“Ϋ®‘Ύ![]() ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«
¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΒΡ”ΑœλΕ»ΈΣ
ΒΡ”ΑœλΕ»ΈΣ![]() Θ§
Θ§
Ε‘≥«![]() ΒΡ”ΑœλΕ»ΈΣ
ΒΡ”ΑœλΕ»ΈΣ![]() Θ§
Θ§
“ρ¥ΥΉή”ΑœλΕ»![]() Θ°
Θ°
”÷“ρΈΣΒ±ά§Μχ¥Πάμ≥ß![]() ”κ≥«
”κ≥«![]() ΨύάκΈΣ
ΨύάκΈΣ![]() ±
±
Ε‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»ΈΣ0.029.
ΒΡΉή”ΑœλΕ»ΈΣ0.029.
Υυ“‘![]() Θ°
Θ°
Υυ“‘![]() Θ°
Θ°
(2)ΓΓ“ρΈΣ![]() Θ°
Θ°
”…![]() ΫβΒΟ
ΫβΒΟ![]() Θ°
Θ°
”…![]() ΫβΒΟ
ΫβΒΟ![]()
”…![]() ΫβΒΟ
ΫβΒΟ![]()
Υυ“‘![]() Θ§
Θ§![]() Υφ
Υφ![]() ΒΡ±δΜ·«ιΩω»γœ¬±μΘΚ
ΒΡ±δΜ·«ιΩω»γœ¬±μΘΚ
|
|
|
|
|
| 0 |
|
| ®K | ΦΪ–Γ÷Β | ®J |
”…±μΩ…÷ΣΘ§Κ· ΐ‘Ύ![]() ΡΎΒΞΒςΒίΦθΘ§‘Ύ
ΡΎΒΞΒςΒίΦθΘ§‘Ύ![]() ΡΎΒΞΒςΒί‘ωΘ§
ΡΎΒΞΒςΒί‘ωΘ§
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Ι ‘ΎœΏΕΈAB…œ¥φ‘Ύ![]() ΒψΘ§ ΙΒΟΫ®‘Ύ¥Υ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«
ΒψΘ§ ΙΒΟΫ®‘Ύ¥Υ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»Ήν–ΓΘ§
ΒΡΉή”ΑœλΕ»Ήν–ΓΘ§
ΗΟΒψ”κ≥«![]() ΒΡΨύάκ
ΒΡΨύάκ![]() Θ°
Θ°


 ΩΈ ±’ΤΩΊΥφΧΟΝΖœΑœΒΝ–¥πΑΗ
ΩΈ ±’ΤΩΊΥφΧΟΝΖœΑœΒΝ–¥πΑΗ “ΜΩΈ“ΜΝΖ“Μ±ΨΆ®œΒΝ–¥πΑΗ
“ΜΩΈ“ΜΝΖ“Μ±ΨΆ®œΒΝ–¥πΑΗ ’ψΫ≠÷°–«―ß“ΒΥ°ΤΫ≤β ‘œΒΝ–¥πΑΗ
’ψΫ≠÷°–«―ß“ΒΥ°ΤΫ≤β ‘œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ÷Ϋ’≈ΒΡΙφΗώ «÷Η÷Ϋ’≈÷Τ≥…ΚσΘ§Ψ≠Ιΐ–ό’ϊ«–±ΏΘ§≤Ο≥…“ΜΕ®ΒΡ≥Ώ¥γ.œ÷‘ΎΈ“Ιζ≤…”ΟΙζΦ ±ξΉΦΘ§ΙφΕ®“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Β»±ξΦ«ά¥±μ Ψ÷Ϋ’≈ΒΡΖυΟφΙφΗώ.Η¥”Γ÷ΫΖυΟφΙφΗώ÷Μ≤…”Ο
Β»±ξΦ«ά¥±μ Ψ÷Ϋ’≈ΒΡΖυΟφΙφΗώ.Η¥”Γ÷ΫΖυΟφΙφΗώ÷Μ≤…”Ο![]() œΒΝ–ΚΆ
œΒΝ–ΚΆ![]() œΒΝ–Θ§Τδ÷–œΒΝ–ΒΡΖυΟφΙφΗώΈΣΘΚΔΌ
œΒΝ–Θ§Τδ÷–œΒΝ–ΒΡΖυΟφΙφΗώΈΣΘΚΔΌ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Υυ”–ΙφΗώΒΡ÷Ϋ’≈ΒΡΖυΩμΘ®“‘
Υυ”–ΙφΗώΒΡ÷Ϋ’≈ΒΡΖυΩμΘ®“‘![]() ±μ ΨΘ©ΚΆ≥ΛΕ»Θ®“‘
±μ ΨΘ©ΚΆ≥ΛΕ»Θ®“‘![]() ±μ ΨΘ©ΒΡ±»άΐΙΊœΒΕΦΈΣ
±μ ΨΘ©ΒΡ±»άΐΙΊœΒΕΦΈΣ![]() ΘΜΔΎΫΪ
ΘΜΔΎΫΪ![]() ÷Ϋ’≈―Ί≥ΛΕ»ΖΫœρΕ‘ΩΣ≥…ΝΫΒ»Ζ÷Θ§±ψ≥…ΈΣ
÷Ϋ’≈―Ί≥ΛΕ»ΖΫœρΕ‘ΩΣ≥…ΝΫΒ»Ζ÷Θ§±ψ≥…ΈΣ![]() ΙφΗώΘ§
ΙφΗώΘ§![]() ÷Ϋ’≈―Ί≥ΛΕ»ΖΫœρΕ‘ΩΣ≥…ΝΫΒ»Ζ÷Θ§±ψ≥…ΈΣ
÷Ϋ’≈―Ί≥ΛΕ»ΖΫœρΕ‘ΩΣ≥…ΝΫΒ»Ζ÷Θ§±ψ≥…ΈΣ![]() ΙφΗώΘ§Γ≠Θ§»γ¥ΥΕ‘ΩΣ÷Ν
ΙφΗώΘ§Γ≠Θ§»γ¥ΥΕ‘ΩΣ÷Ν![]() ΙφΗώ.œ÷”–
ΙφΗώ.œ÷”–![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷ΫΗς“Μ’≈.»τ
÷ΫΗς“Μ’≈.»τ![]() ÷ΫΒΡΩμΕ»ΈΣ
÷ΫΒΡΩμΕ»ΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ÷ΫΒΡΟφΜΐΈΣ________
÷ΫΒΡΟφΜΐΈΣ________![]() ΘΜ’β
ΘΜ’β![]() ’≈÷ΫΒΡΟφΜΐ÷°ΚΆΒ»”Ύ________
’≈÷ΫΒΡΟφΜΐ÷°ΚΆΒ»”Ύ________![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Αύ…œΈγ”–ΈεΫΎΩΈΘ§Ζ÷³eΑ≤≈≈”οΈΡΘ§ ΐ―ßΘ§”Δ”οΘ§ΈοάμΘ§Μ·―ßΗς“ΜΫΎΩΈΘ°“Σ«σ”οΈΡ”κΜ·―ßœύΝΎΘ§ ΐ―ß”κΈοάμ≤ΜœύΝΎΘ§«“ ΐ―ßΩΈ≤Μ≈≈ΒΎ“ΜΫΎΘ§‘ρ≤ΜΆ§≈≈ΩΈΖ®ΒΡ÷÷ ΐ «
A. 24B. 16C. 8D. 12
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2021ΡξΈ“ ΓΫΪ Β ©–¬ΗΏΩΦΘ§–¬ΗΏΩΦΓΑ“άΨίΆ≥“ΜΗΏΩΦ≥…Φ®ΓΔΗΏ÷–―ß“ΒΥ°ΤΫΩΦ ‘≥…Φ®Θ§≤ΈΩΦΗΏ÷–―ß…ζΉέΚœΥΊ÷ ΤάΦέ–≈œΔΓ±Ϋχ––»Υ≤≈―ΓΑΈΓΘΈ“–Θ2018ΦΕΗΏ“ΜΡξΦΕ“ΜΗω―ßœΑ–Υ»Λ–ΓΉιΫχ––…γΜα ΒΦυΜνΕ·Θ§ΨωΕ®Ε‘Ρ≥…Χ≥Γœζ έΒΡ…ΧΤΖAΫχ–– –≥Γœζ έΝΩΒς―–Θ§Ά®ΙΐΕ‘ΗΟ…ΧΤΖ“ΜΗωΫΉΕΈΒΡΒς―–ΒΟ÷ΣΘ§ΖΔœ÷ΗΟ…ΧΤΖΟΩ»’ΒΡœζ έΝΩ![]() Θ®ΒΞΈΜΘΚΑΌΦΰΘ©”κœζ έΦέΗώ
Θ®ΒΞΈΜΘΚΑΌΦΰΘ©”κœζ έΦέΗώ![]() Θ®‘Σ/ΦΰΘ©ΫϋΥΤ¬ζΉψΙΊœΒ Ϋ
Θ®‘Σ/ΦΰΘ©ΫϋΥΤ¬ζΉψΙΊœΒ Ϋ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() ΈΣ≥Θ ΐ
ΈΣ≥Θ ΐ![]() “―÷Σœζ έΦέΗώΈΣ3‘Σ/Φΰ ±Θ§ΟΩ»’Ω… έ≥ωΗΟ…ΧΤΖ10ΑΌΦΰΓΘ
“―÷Σœζ έΦέΗώΈΣ3‘Σ/Φΰ ±Θ§ΟΩ»’Ω… έ≥ωΗΟ…ΧΤΖ10ΑΌΦΰΓΘ
(1)«σΚ· ΐ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
(2)»τΗΟ…ΧΤΖAΒΡ≥…±ΨΈΣ2‘Σ/ΦΰΘ§ΗυΨίΒς―–ΫαΙϊ«κΡψ ‘»ΖΕ®ΗΟ…ΧΤΖœζ έΦέΗώΒΡ÷ΒΘ§ ΙΗΟ…Χ≥ΓΟΩ»’œζ έΗΟ…ΧΤΖΥυΜώΒΟΒΡάϊ»σΘ®ΒΞΈΜΘΚΑΌ‘ΣΘ©Ήν¥σΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§Ϋ«AΘ§BΘ§CΥυΕ‘ΒΡ±ΏΖ÷±πΈΣaΘ§bΘ§cΘ§¬ζΉψ(2b©¹c)cosAΘΫacosCΘ°
Θ®1Θ©«σΫ«AΘΜ
Θ®2Θ©»τ![]() Θ§b+cΘΫ5Θ§«σΓςABCΒΡΟφΜΐΘ°
Θ§b+cΘΫ5Θ§«σΓςABCΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕ®“ε‘ΎR…œΒΡΚ· ΐfΘ®xΘ©ΘΫ|x©¹m|+|x|Θ§mΓ N*Θ§¥φ‘Ύ Β ΐx ΙfΘ®xΘ©ΘΦ2≥…ΝΔΘ°
Θ®1Θ©«σ≤ΜΒ» ΫfΘ®xΘ©ΘΨ8ΒΡΫβΘΜ
Θ®2Θ©»τΠΝΘ§Π¬Γί1Θ§fΘ®ΠΝΘ©+fΘ®Π¬Θ©ΘΫ4Θ§«σ÷ΛΘΚ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
Θ®1Θ©Χ÷¬έ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®2Θ©»τ![]() ‘ΎΕ®“ε”ρΡΎ”–ΝΫΗωΦΪ÷ΒΒψ
‘ΎΕ®“ε”ρΡΎ”–ΝΫΗωΦΪ÷ΒΒψ![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύάβ≥ΛΈΣ1ΒΡ’ΐΖΫΧε![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() «Ε‘Ϋ«œΏ
«Ε‘Ϋ«œΏ![]() …œΒΡΕ·ΒψΘ®Βψ
…œΒΡΕ·ΒψΘ®Βψ![]() ”κ
”κ![]() ≤Μ÷ΊΚœΘ©Θ§‘ρœ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «____.
≤Μ÷ΊΚœΘ©Θ§‘ρœ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «____.
ΔΌ¥φ‘ΎΒψ![]() Θ§ ΙΒΟΤΫΟφ
Θ§ ΙΒΟΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
ΔΎ¥φ‘ΎΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Δέ![]() ΒΡΟφΜΐ≤ΜΩ…ΡήΒ»”Ύ
ΒΡΟφΜΐ≤ΜΩ…ΡήΒ»”Ύ![]() ΘΜ
ΘΜ
Δή»τ![]() Ζ÷±π «
Ζ÷±π «![]() ‘ΎΤΫΟφ
‘ΎΤΫΟφ![]() ”κΤΫΟφ
”κΤΫΟφ![]() ΒΡ’ΐΆΕ”ΑΒΡΟφΜΐΘ§‘ρ¥φ‘ΎΒψ
ΒΡ’ΐΆΕ”ΑΒΡΟφΜΐΘ§‘ρ¥φ‘ΎΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
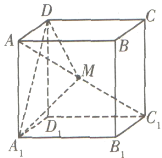
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψH‘Ύ’ΐΖΫΧε![]() ΒΡΕ‘Ϋ«œΏ
ΒΡΕ‘Ϋ«œΏ![]() …œΘ§ΓœHDA=
…œΘ§ΓœHDA=![]() Θ°
Θ°

Θ®1Θ©«σDH”κ![]() Υυ≥…Ϋ«ΒΡ¥σ–ΓΘΜ
Υυ≥…Ϋ«ΒΡ¥σ–ΓΘΜ
Θ®2Θ©«σDH”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com