【题目】如图所示，在以
为直径的半圆周上，有异于
的六个点
，直径上有异于的四个点
.则：
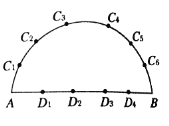
（1）以这12个点（包括）中的4个点为顶点，可作出多少个四边形？
（2）以这10个点（不包括）中的3个点为顶点，可作出多少个三角形？
名校通行证有效作业系列答案科目：高中数学 来源： 题型：
【题目】某班50名学生在一次百米测试中，成绩全部介于13 s与19 s之间，将测试结果分成如下六组：[13,14)，[14,15)，[15,16)，[16,17)，[17,18)，[18,19]．如图是按上述分组方法得到的频率分布直方图，设成绩小于17 s的学生人数占全班人数的百分比为x，成绩在[15,17)中的学生人数为y，则从频率分布直方图中可以分析出x和y分别为 ( )
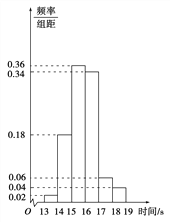
A. 90%,35B. 90%,45
C. 10%,35D. 10%,45
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，内角A、B、C所对的边为a、b、c，且 
asinC﹣c（2+cosA）=0．
（1）求角A的大小；
（2）若△ABC的最大边长为 
，且sinC=2sinB，求最小边长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（ω＞0）的最小正周期为π．
（Ⅰ）求ω的值和f（x）的单调递增区间；
（Ⅱ）若关于x的方程f（x）﹣m＝0在区间[0，
]上有两个实数解，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】假设每一架飞机的每一个引擎在飞行中出现故障概率均为
，且各引擎是否有故障是独立的，已知4引擎飞机中至少有3个引擎飞机正常运行，飞机就可成功飞行；2引擎飞机要2个引擎全部正常运行，飞机才可成功飞行.要使4引擎飞机比2引擎飞机更安全，则
的取值范围是__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】意大利著名数学家斐波那契在研究兔子的繁殖问题时，发现有这样的一列数：1，1，2，3，5，8，…，该数列的特点是：前两个数均为1，从第三个数起，每一个数都等于它前面两个数的和．人们把这样的一列数组成的数列{an}称为斐波那契数列，则 
﹣ 
=（ ）
A.0
B.﹣1
C.1
D.2
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c，且满足sin2B+sin2C=sin2A+2sinBsinCsin（B+C）． （Ⅰ）求角A的大小；
（Ⅱ）若a=2，求△ABC面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如下茎叶图：
（1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；
（2）求40名工人完成生产任务所需时间的中位数
，并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
（3）根据（2）中的列联表，能否有99%的把握认为两种生产方式的效率有差异？
附：
，
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两组各有三名同学，他们在一次测试中的成绩分别为：甲组：88、89、90；乙组：87、88、92．如果分别从甲、乙两组中随机选取一名同学，则这两名同学的成绩之差的绝对值不超过3的概率是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
