分析:(I)在
=S2n-1中,令n=1,n=2,得
,解得a
n=2n-1,由足
bn==
(-),能求出a
1,d和T
n.
(II)当n为偶数时,要使不等式
λTn<n+8•(-1)n恒成立,即需不等式
λ<=2n++17恒成立.由此解得λ<25;当n为奇数时,要使不等式
λTn<n+8•(-1)n恒成立,需不等式
λ<=2n--15恒成立,解得λ<-21.由此能够求出λ的取值范围.
解答:解:(I)在
=S2n-1中,令n=1,n=2,
得
,即
,
解得a
1=1,d=2,(3分)
| | ∴an=2n-1. | | ∵bn===(-), | | ∴Tn=(1-+-+…+-)=.…(6分) |
| |
(II)(1)当n为偶数时,要使不等式
λTn<n+8•(-1)n恒成立,
即需不等式
λ<=2n++17恒成立.
∵
2n+≥8,等号在n=2时取得.
∴此时λ需满足λ<25.(8分)
(2)当n为奇数时,要使不等式
λTn<n+8•(-1)n恒成立,
即需不等式
λ<=2n--15恒成立.
∵
2n-是随n的增大而增大,
∴
n=1时2n-取得最小值-6.
∴此时λ需满足λ<-21.(10分)
综合(1)(2)可得λ<-21
∴λ的取值范围是{λ|λ<-21}.(12分)
点评:本题考查等差数列的首项、公差的求法,考查数列前n项和的求法,考查实数的取值范围的求法,考查数列与不等式的综合运用.解题时要认真审题,注意迭代法、裂项求和法、等价转化法的合理运用.



 名校课堂系列答案
名校课堂系列答案 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足xnan=xn+1an+1=xn+2an+2(n∈N*).
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足xnan=xn+1an+1=xn+2an+2(n∈N*). 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足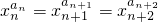 (n∈N*).
(n∈N*).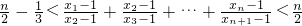 .
. (n∈N*).
(n∈N*). .
.
 (n∈N*).
(n∈N*). .
.