
【题目】设椭圆![]() 的焦点
的焦点![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,若
两点,若![]() 的周长为短轴长的
的周长为短轴长的![]() 倍.
倍.
(1)求![]() 的离心率;
的离心率;
(2)设![]() 的斜率为
的斜率为![]() ,在
,在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标; 若不存在,说明理由.
的坐标; 若不存在,说明理由.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒, 以防止害虫的危害, 但采集上市时蔬菜仍存有少量的残留农药, 食用时需要用清水清洗干净, 下表是用清水![]() (单位:千克) 清洗该蔬菜
(单位:千克) 清洗该蔬菜![]() 千克后, 蔬菜上残留的农药
千克后, 蔬菜上残留的农药![]() (单位:微克) 的统计表:
(单位:微克) 的统计表:
|
|
|
|
|
|
|
|
|
|
|
|
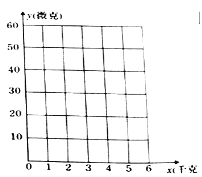
(1)在下面的坐标系中, 描出散点图, 并判断变量![]() 与
与![]() 的相关性;
的相关性;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程, 令
的回归方程, 令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中) ,求出
,完成以下表格(填在答题卡中) ,求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() 精确到
精确到![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于![]() 微克时对人体无害, 为了放心食用该蔬菜, 请
微克时对人体无害, 为了放心食用该蔬菜, 请
估计需要用多少千克的清水清洗一千克蔬菜?(精确到![]() ,参考数据
,参考数据![]() )
)
(附:线性回归方程![]() 中系数计算公式分别为;
中系数计算公式分别为;
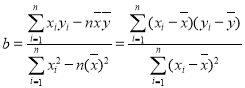 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)完游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)设![]() 分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况;
分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况;
(2)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜,你认为此游戏是否公平,说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图(如图所示),已知图中从左到右前三个小组的频率分别时0.1,0.3,0.4,第一小组的频数为5.
(1)求第四小组的频率?
(2)问参加这次测试的学生人数是多少?
(3)问在这次测试中,学生跳绳次数的中位数落在第几小组内?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于空间直角坐标系![]() 中的一点
中的一点![]() ,有下列说法:
,有下列说法:
①点![]() 到坐标原点的距离为
到坐标原点的距离为![]() ;
;
②![]() 的中点坐标为
的中点坐标为![]() ;
;
③点![]() 关于
关于![]() 轴对称的点的坐标为
轴对称的点的坐标为![]() ;
;
④点![]() 关于坐标原点对称的点的坐标为
关于坐标原点对称的点的坐标为![]() ;
;
⑤点![]() 关于坐标平面
关于坐标平面![]() 对称的点的坐标为
对称的点的坐标为![]() .
.
其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com