
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| asinB |
| sinA |
| asinC |
| sinA |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 2 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
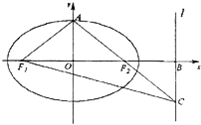 如图,椭圆
如图,椭圆| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、X+Z=2Y |
| B、Y(Y-X)=Z(Z-X) |
| C、Y2=XZ |
| D、Y(Y-X)=X(Z-X) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| A、3 | B、2 | C、1 | D、0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、一个骰子掷一次得到2点的概率为
| ||
| B、某地气象台预报说,明天本地降水的概率为70%,这说明明天本地有70%的区域下雨,30%的区域不下雨 | ||
| C、某中学高二年级有12个班,要从中选2个班参加活动.由于某种原因,一班必须参加,另外再从二至十二班中选一个班,有人提议用如下方法:掷两个骰子得到的点数和是几,就选几班,这是很公平的方法 | ||
| D、在一场乒乓球赛前,裁判一般用掷硬币猜正反面来决定谁先发球,这应该说是公平的 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a15 |
| a14 |
| A、S14必为Sn的最大值 |
| B、S14必为Sn的最小值 |
| C、S15必为Sn的最大值 |
| D、S14可能为Sn的最大值,也可能为Sn的最小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com