
分析 (Ⅰ)法一:求出双曲线的焦点坐标,利用双曲线定义求出a,然后求双曲线C的方程,渐近线方程.
法二:利用已知条件列出方程组,求出a,b,然后求双曲线C的方程,渐近线方程.
(Ⅱ)联立$\left\{\begin{array}{l}y=kx-1\\ 3{x^2}-{y^2}=3\end{array}\right.$利用△>0,求出-2<k<2,结合渐近线求解k的范围即可.
解答 (本小题满分12分)
解:(Ⅰ)法一:由已知,双曲线的焦点为(-2,0)和(2,0)…(1分)
据定义有:$2a=|\sqrt{{{(2+2)}^2}+{{(3-0)}^2}}-\sqrt{{{(2-2)}^2}+{{(3-0)}^2}}|=2⇒a=1$…(2分)
故a2=1,c2=4,b2=3,从而所求双曲线C的方程为${x^2}-\frac{y^2}{3}=1$.…(4分)
其渐近线方程为:$y=±\sqrt{3}x$…(6分)
法二:由$\left\{\begin{array}{l}\frac{4}{a^2}-\frac{9}{b^2}=1\\{a^2}+{b^2}=4\end{array}\right.⇒\left\{\begin{array}{l}{a^2}=1\\{b^2}=3\end{array}\right.$,故所求双曲线C的方程为${x^2}-\frac{y^2}{3}=1$…(4分)
其渐近线方程为:$y=±\sqrt{3}x$…(6分)
(Ⅱ)由$\left\{\begin{array}{l}y=kx-1\\ 3{x^2}-{y^2}=3\end{array}\right.$得:(3-k2)x2+2kx-4=0…(8分)
当3-k2≠0,即$k≠±\sqrt{3}$时,…(9分)
若△>0,即△=4k2-4(-4)(3-k2)=12(4-k2)>0⇒4-k2>0⇒-2<k<2时,
直线与双曲线相交,有两个公共点;…(11分)
所以,当-2<k<2,且$k≠±\sqrt{3}$时,直线与双曲线有两个公共点.…(12分)
点评 本题考查双曲线的简单性质以及双曲线方程的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
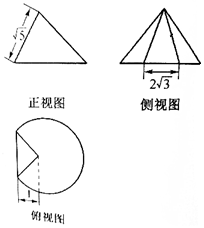 一个圆锥被过顶点的平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过顶点的平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )| A. | $\frac{8π}{3}$+$\sqrt{15}$ | B. | $\frac{16π}{3}$+$\sqrt{3}$ | C. | $\frac{8π}{3}$+$\frac{2\sqrt{3}}{3}$ | D. | $\frac{16π}{9}$+$\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
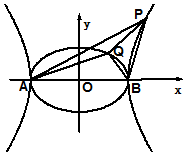 已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点,P、Q分别为双曲线和椭圆上不同于两点A、B的动点,且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ($\overrightarrow{OA}$+$\overrightarrow{QB}$)(λ∈R,|λ|>1),设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4的值( )
已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点,P、Q分别为双曲线和椭圆上不同于两点A、B的动点,且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ($\overrightarrow{OA}$+$\overrightarrow{QB}$)(λ∈R,|λ|>1),设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4的值( )| A. | 大于0 | B. | 等于0 | ||
| C. | 小于0 | D. | 大于0,等于0,小于0都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
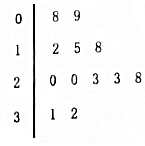 广安市2015年每个月平均气温(摄氏度)数据茎叶图如图,则这组数据的中位数、众数分别是( )
广安市2015年每个月平均气温(摄氏度)数据茎叶图如图,则这组数据的中位数、众数分别是( )| A. | 20;23 | B. | 21.5;20,23 | C. | 20;20,23 | D. | 21.5;23 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
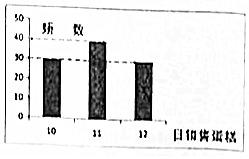 某超市每两天购入一批某型号的生日蛋糕进行销售,进价50元/个,售价60元/个,若每次购入的生日蛋糕两天内没有售完,则以40元/个的价格可以全部处理掉,根据此超市以往随机抽取的100天此类蛋糕的销售情况,如柱形图所示.设n为每次购入的蛋糕数,ξ为两天内的蛋糕销售数量,W为此批购入的蛋糕销售的利润(视频率为概率,且每天销售情况是独立的)
某超市每两天购入一批某型号的生日蛋糕进行销售,进价50元/个,售价60元/个,若每次购入的生日蛋糕两天内没有售完,则以40元/个的价格可以全部处理掉,根据此超市以往随机抽取的100天此类蛋糕的销售情况,如柱形图所示.设n为每次购入的蛋糕数,ξ为两天内的蛋糕销售数量,W为此批购入的蛋糕销售的利润(视频率为概率,且每天销售情况是独立的)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{12}$ | C. | $\frac{7\sqrt{3}}{12}$ | D. | -$\frac{7\sqrt{3}}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com