
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() C的极坐标方程为
C的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 分别交
分别交![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程![]() 1表示焦点在x轴上的双曲线.
1表示焦点在x轴上的双曲线.
(1)命题q为真命题,求实数k的取值范围;
(2)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点在x轴上,中心在坐标原点,离心率![]() ,椭圆上的点到左焦点的距离的最大值为
,椭圆上的点到左焦点的距离的最大值为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆的右焦点F作与坐标轴不垂直的直线l,交椭圆于A、B两点,设点![]() 是线段OF上的一个动点,且
是线段OF上的一个动点,且![]() ,求m的取值范围;
,求m的取值范围;
(3)设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C、B、N三点共线?若存在,求出定点N的坐标,若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某老小区建成时间较早,没有集中供暖,随着人们生活水平的日益提高热力公司决定在此小区加装暖气该小区的物业公司统计了近五年(截止2018年年底)小区居民有意向加装暖气的户数,得到如下数据
年份编号x | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
加装户数y | 34 | 95 | 124 | 181 | 216 |
(Ⅰ)若有意向加装暖气的户数y与年份编号x满足线性相关关系求y与x的线性回归方程并预测截至2019年年底,该小区有多少户居民有意向加装暖气;
(Ⅱ)2018年年底郑州市民生工程决定对老旧小区加装暖气进行补贴,该小区分到120个名额物业公司决定在2019年度采用网络竞拍的方式分配名额,竞拍方案如下:①截至2018年年底已登记在册的居民拥有竞拍资格;②每户至多申请一个名额,由户主在竞拍网站上提出申请并给出每平方米的心理期望报价;③根据物价部门的规定,每平方米的初装价格不得超过300元;④申请阶段截止后,将所有申请居民的报价自高到低排列,排在前120位的业主以其报价成交;⑤若最后出现并列的报价,则认为申请时问在前的居民得到名额,为预测本次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的50位居民进行调查统计了他们的拟报竞价,得到如图所示的频率分布直方图:

(1)求所抽取的居民中拟报竞价不低于成本价180元的人数;
(2)如果所有符合条件的居民均参与竞拍,请你利用样本估计总体的思想预测至少需要报价多少元才能获得名额(结果取整数)
参考公式对于一组数据(x1,y1),(x2,y2),(x3,y3),…(xn,yn),其回归直线![]() 的斜率和截距的最小二乘估计分别为,
的斜率和截距的最小二乘估计分别为,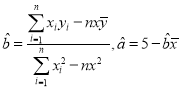
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为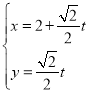 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】材料一:2018年,全国逾半省份将从秋季入学的高一年级开始实行新的学业水平考试和高考制度.所有省级行政区域均突破文理界限,由学生跨文理选科,均设 置“![]() ”的考试科目.前一个“3”为必考科目,为统一高考科目语文、数学、外语.除个别省级行政区域仍执行教育部委托的分省命题任务外,绝大部分省级行政区域均由教育部考试中心统一命题;后一个“3”为高中学业水平考试(简称“学考”)选考科目,由各省级行政区域自主命题.材料二:2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,方案决定从2018年秋季入学的高中一年级学生开始实施高考综合改革.考生总成绩由全国统一高考的语文、数学、外语3个科目成绩和考生选择的3科普通高中学业水平选择性考试科目成绩组成,满分为750分.即通常所说的“
”的考试科目.前一个“3”为必考科目,为统一高考科目语文、数学、外语.除个别省级行政区域仍执行教育部委托的分省命题任务外,绝大部分省级行政区域均由教育部考试中心统一命题;后一个“3”为高中学业水平考试(简称“学考”)选考科目,由各省级行政区域自主命题.材料二:2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,方案决定从2018年秋季入学的高中一年级学生开始实施高考综合改革.考生总成绩由全国统一高考的语文、数学、外语3个科目成绩和考生选择的3科普通高中学业水平选择性考试科目成绩组成,满分为750分.即通常所说的“![]() ”模式,所谓“
”模式,所谓“![]() ”,即“3”是三门主科,分别是语文、数学、外语,这三门科目是必选的.“1”指的是要在物理、历史里选一门,按原始分计入成绩.“2”指考生要在生物、化学、思想政治、地理4门中选择2门.但是这几门科目不以原始分计入成绩,而是等级赋分.等级赋分指的是把考生的原始成绩根据人数的比例分为
”,即“3”是三门主科,分别是语文、数学、外语,这三门科目是必选的.“1”指的是要在物理、历史里选一门,按原始分计入成绩.“2”指考生要在生物、化学、思想政治、地理4门中选择2门.但是这几门科目不以原始分计入成绩,而是等级赋分.等级赋分指的是把考生的原始成绩根据人数的比例分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级,五个等级分别对应着相应的分数区间,然后再用公式换算,转换得出分数.
五个等级,五个等级分别对应着相应的分数区间,然后再用公式换算,转换得出分数.
(1)若按照“![]() ”模式选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
”模式选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
(2)某教育部门为了调查学生语数外三科成绩与选科之间的关系,现从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,满分450分,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分;
①考生甲得知他的成绩为270分,考试后不久了解到如下情况:“此次测试平均成绩为171分,351分以上共有57人”,问甲能否获得荣誉证书,请说明理由;
②考生丙得知他的实际成绩为430分,而考生乙告诉考生丙:“这次测试平均成绩为201分,351分以上共有57人”,请结合统计学知识帮助丙同学辨别乙同学 信息的真伪.
附:![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
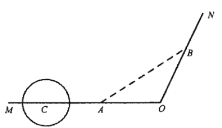
【题目】为解决城市的拥堵问题,某城市准备对现有的一条穿城公路![]() 进行分流,已知穿城公路
进行分流,已知穿城公路![]() 自西向东到达城市中心
自西向东到达城市中心![]() 后转向
后转向![]() 方向,已知
方向,已知![]() ,现准备修建一条城市高架道路
,现准备修建一条城市高架道路![]() ,
,![]() 在
在![]() 上设一出入口
上设一出入口![]() ,在
,在![]() 上设一出口
上设一出口![]() ,假设高架道路
,假设高架道路![]() 在
在![]() 部分为直线段,且要求市中心
部分为直线段,且要求市中心![]() 与
与![]() 的距离为
的距离为![]() .
.
(1)若![]() ,求两站点
,求两站点![]() 之间的距离;
之间的距离;
(2)公路![]() 段上距离市中心
段上距离市中心![]()
![]() 处有一古建筑群
处有一古建筑群![]() ,为保护古建筑群,设立一个以
,为保护古建筑群,设立一个以![]() 为圆心,
为圆心,![]() 为半径的圆形保护区.因考虑未来道路
为半径的圆形保护区.因考虑未来道路![]() 的扩建,则如何在古建筑群和市中心
的扩建,则如何在古建筑群和市中心![]() 之间设计出入口
之间设计出入口![]() ,才能使高架道路及其延伸段不经过保护区?
,才能使高架道路及其延伸段不经过保护区?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com