
分析 以MNP为底面,Q为顶点,则:四面体MNPQ的体积V=$\frac{1}{3}$hS,其中:h是Q点到底面的距离,是定值,h=a,于是,要使得V最大,等价于使得底面△MNP的面积S最大.
解答 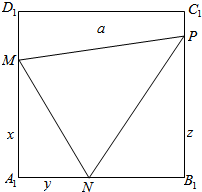 解:以MNP为底面,Q为顶点,则:四面体MNPQ的体积V=$\frac{1}{3}$hS
解:以MNP为底面,Q为顶点,则:四面体MNPQ的体积V=$\frac{1}{3}$hS
其中:h是Q点到底面的距离,是定值,h=a,
于是,要使得V最大,等价于使得底面△MNP的面积S最大.
设A1M=x,A1N=y,B1P=z,(0≤x,y,z≤a)则:
S=S正方形-${S}_{△{A}_{1}MN}$-${S}_{△{B}_{1}NP}$-${S}_{梯形{C}_{1}{D}_{1}MP}$
=a2-$\frac{1}{2}$xy-$\frac{1}{2}$(a-y)z-$\frac{1}{2}$a(a-x+a-z)
=a2-$\frac{1}{2}$xy-$\frac{1}{2}$(a-y)z-a2+$\frac{1}{2}$a(x+z)
=$\frac{1}{2}$(ax-xy+yz)
≤$\frac{1}{2}$[x(a-y)+ya]
≤$\frac{1}{2}$[a(a-y)+ya]
=$\frac{1}{2}$a2
即:S的最大值=$\frac{1}{2}$a2(此时,x=z=a,b可随意)
故:四面体MNPQ的体积V的最大值=$\frac{1}{3}$aS=$\frac{1}{6}$a3,
故答案为:$\frac{1}{6}$a3.
点评 本题考查四面体MNPQ的体积V的最大值,考查学生分析解决问题的能力,要使得V最大,等价于使得底面△MNP的面积S最大是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-2$\sqrt{5}$+3) | B. | (-∞,-2$\sqrt{5}$+3) | C. | (-$\frac{1}{2}$,4-$\sqrt{17}$) | D. | (-∞,4-$\sqrt{17}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )
如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )| A. | [0,$\frac{\sqrt{2}}{8}$]∪($\frac{5\sqrt{2}}{8}$,1) | B. | [$\frac{\sqrt{2}}{8}$,$\frac{5\sqrt{2}}{8}$] | C. | [0,$\frac{\sqrt{2}}{8}$] | D. | [0,$\frac{5\sqrt{2}}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|kπ-$\frac{π}{12}$<x<kπ+$\frac{π}{4}$,k∈Z} | B. | {x|kπ+$\frac{π}{4}$<x<kπ+$\frac{11π}{12}$,k∈Z} | ||
| C. | {x|kπ-$\frac{π}{6}$<x<kπ+$\frac{π}{2}$,k∈Z} | D. | {x|kπ<x<kπ+$\frac{π}{3}$,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com