
【题目】函数f(x)=2ax2﹣2bx﹣a+b(a,b∈R,a>0),g(x)=2ax﹣2b
(1)若![]() 时,求f(sinθ)的最大值;
时,求f(sinθ)的最大值;
(2)设a>0时,若对任意θ∈R,都有|f(sinθ)|≤1恒成立,且g(sinθ)的最大值为2,求f(x)的表达式.
【答案】解:(1)令sinθ=t∈[0,1],问题等价于求f(t)=2at2﹣2bt﹣a+b在t∈[0,1]的最大值,
∵a>0,抛物线开口向上,二次函数的对称轴t=![]() ,
,
由二次函数区间的最值可得![]()
(2)令sinθ=t∈[﹣1,1],则|f(t)|≤1可推得|f(0)|≤1,|f(1)|≤1,|f(﹣1)|≤1,
∵a>0,∴g(sinθ)max=g(1)=2,而g(1)=2a﹣2b=2
而f(0)=b﹣a=﹣1而t∈[﹣1,1]时,|f(t)|≤1,即﹣1≤f(t)≤1,
结合f(0)=﹣1可知二次函数的顶点坐标为(0,﹣1)
∴b=0,a=1,∴f(x)=2x2﹣1.
【解析】(1)令sinθ=t∈[0,1],问题等价于求f(t)=2at2﹣2bt﹣a+b在t∈[0,1]的最大值,由二次函数区间的最值可得;
(2)令sinθ=t∈[﹣1,1],由恒成立和最大值可得可得二次函数的顶点坐标为(0,﹣1),进而可得ab的值,可得解析式.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() (
(![]() ).
).
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
, ![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() 均有
均有![]() 恒成立;
恒成立;
(3)设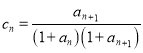 ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意
项和,若对任意![]() 均有
均有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设角A,B,C的对边分别为a,b,c,向量![]() =(cosA,sinA),
=(cosA,sinA),![]() =(
=(![]() ﹣sinA,cosA),若
﹣sinA,cosA),若![]()
![]() =1.
=1.
(1)求角A的大小;
(2)若b=4![]() , 且c=
, 且c=![]() a,求△ABC的面积.
a,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是![]() .
.
(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当λ=4时,记动点P的轨迹为曲线D.F,G是曲线D上不同的两点,对于定点Q(﹣3,0),有|QF||QG|=4.试问无论F,G两点的位置怎样,直线FG能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(3+x)+ln(3﹣x).
(Ⅰ)求函数y=f(x)的定义域;
(Ⅱ)判断函数y=f(x)的奇偶性;
(Ⅲ)若f(2m﹣1)<f(m),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
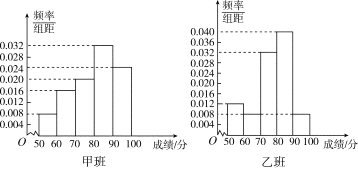
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com