
°æƒø°øŒ™¡À»√∆∂¿ßµÿ«¯µƒ∫¢◊”√«π˝“ª∏ˆŒ¬≈صƒ∂¨ÃÏ£¨ƒ≥–£—Ùπ‚÷æ‘∏’þ…ÁÕ≈◊È÷Ø°∞’‚∏ˆ∂¨ÃÏ≤ª‘Ÿ¿‰°±∂¨“¬ƒºæ˪Ó∂Ø£¨π≤”–50√˚÷æ‘∏’þ≤Œ”Î.÷æ‘∏’þµƒπ§◊˜ƒ⁄»ð”–¡ΩœÓ£∫¢ŸµΩ∏˜∞ý◊ˆ–˚¥´£¨≥´“ÈÕ¨—ß√«ª˝º´æËœ◊∂¨“¬£ª¢⁄’˚¿Ì°¢¥Ú∞¸ƒºæË…œ¿¥µƒ“¬ŒÔ.√øŒª÷æ‘∏’þ∏˘æð◊‘…Ì µº «Èøˆ£¨÷ª≤Œ”Î∆‰÷–µƒƒ≥“ªœÓπ§◊˜.œýπÿÕ≥º∆ ˝æð»Áœ¬±ÌÀ˘ æ£∫

£®1£©»Áπ˚”√∑÷≤„≥È—˘µƒ∑Ω∑®¥”≤Œ”Î¡ΩœÓπ§◊˜µƒ÷æ‘∏’þ÷–≥È»°5»À£¨‘Ÿ¥”’‚5»À÷–—°2»À£¨ƒ«√¥°∞÷¡…Ÿ”–1»À «≤Œ”Î∞ýº∂–˚¥´µƒ÷æ‘∏’þ°±µƒ∏≈¬ «∂ý…Ÿ£ø
£®2£©»Ù≤Œ”Î∞ýº∂–˚¥´µƒ÷æ‘∏’þ÷–”–12√˚ƒ–…˙£¨8√˚≈Æ…˙£¨¥”÷–—°≥ˆ2√˚÷æ‘∏’þ£¨”√![]() ±Ì æÀ˘—°÷æ‘∏’þ÷–µƒ≈Æ…˙»À ˝£¨–¥≥ˆÀʪ˙±‰¡ø
±Ì æÀ˘—°÷æ‘∏’þ÷–µƒ≈Æ…˙»À ˝£¨–¥≥ˆÀʪ˙±‰¡ø![]() µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚£Æ
µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚£Æ
°æ¥∞∏°ø£®¢Ò£©![]() £ª£®¢Ú£©
£ª£®¢Ú£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®¢Ò£©”…∑÷≤„≥È—˘∑Ω∑®µ√≤Œ”εΩ∞ýº∂–˚¥´µƒ÷æ‘∏’þ±ª≥È÷–µƒ”–2»À£¨≤Œ”Î’˚¿Ì°¢¥Ú∞¸“¬ŒÔ’þ±ª≥È÷–µƒ”–3»À£¨”…¥ÀƒÐ«Û≥ˆ÷¡…Ÿ”–1»À «≤Œ”Î∞ýº∂–˚¥´µƒ÷æ‘∏’þµƒ∏≈¬ £Æ
£®¢Ú£©≈Æ…˙÷æ‘∏’þ»À ˝X=0£¨1£¨2£¨∑÷±«Û≥ˆ∆‰∏≈¬ £¨”…¥ÀƒÐ«Û≥ˆÀʪ˙±‰¡øXµƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚£Æ
°æΩ‚¥°ø£®¢Ò£©Ω‚£∫”√∑÷≤„≥È—˘∑Ω∑®£¨√ø∏ˆ»À≥È÷–µƒ∏≈¬ «![]() £¨
£¨
°ý≤Œ”εΩ∞ýº∂–˚¥´µƒ÷æ‘∏’þ±ª≥È÷–µƒ”–20°¡![]() =2»À£¨
=2»À£¨
≤Œ”Î’˚¿Ì°¢¥Ú∞¸“¬ŒÔ’þ±ª≥È÷–µƒ”–30°¡![]() =3»À£¨
=3»À£¨
π °∞÷¡…Ÿ”–1»À «≤Œ”Î∞ýº∂–˚¥´µƒ÷æ‘∏’þ°±µƒ∏≈¬ Œ™£∫P=1©Å![]() =
=![]() £Æ
£Æ
£®¢Ú£©Ω‚£∫≈Æ…˙÷æ‘∏’þ»À ˝X=0£¨1£¨2£¨
‘Ú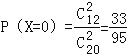 £¨
£¨
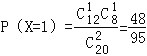 £¨
£¨
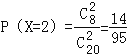 £¨
£¨
°ýXµƒ∑÷≤º¡–Œ™£∫

°ýXµƒ ˝—ß∆⁄Õ˚EX=![]() =
=![]() £Æ
£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∆Û“µ…˙≤˙º◊°¢““¡Ω÷÷≤˙∆∑£¨œ˙ €¿˚»Û∑÷±Œ™2«ß‘™/º˛°¢1«ß‘™/º˛.º◊°¢““¡Ω÷÷≤˙∆∑∂º–Ë“™‘⁄![]() ¡Ω÷÷…˱∏…œº”𧣨…˙≤˙“ªº˛º◊≤˙∆∑–Ë”√
¡Ω÷÷…˱∏…œº”𧣨…˙≤˙“ªº˛º◊≤˙∆∑–Ë”√![]() …˱∏2–° ±£¨
…˱∏2–° ±£¨ ![]() …˱∏6–° ±£ª…˙≤˙“ªº˛““≤˙∆∑–Ë”√
…˱∏6–° ±£ª…˙≤˙“ªº˛““≤˙∆∑–Ë”√![]() …˱∏3–° ±£¨
…˱∏3–° ±£¨ ![]() …˱∏1–° ±.
…˱∏1–° ±. ![]() ¡Ω÷÷…˱∏√ø‘¬ø… π”√ ±º‰ ˝∑÷±Œ™480–° ±°¢960–° ±£¨»Ù…˙≤˙µƒ≤˙∆∑∂ºƒÐº∞ ± €≥ˆ£¨‘Ú∏√∆Û“µ√ø‘¬¿˚»Ûµƒ◊Ó¥Û÷µŒ™£® £©
¡Ω÷÷…˱∏√ø‘¬ø… π”√ ±º‰ ˝∑÷±Œ™480–° ±°¢960–° ±£¨»Ù…˙≤˙µƒ≤˙∆∑∂ºƒÐº∞ ± €≥ˆ£¨‘Ú∏√∆Û“µ√ø‘¬¿˚»Ûµƒ◊Ó¥Û÷µŒ™£® £©
A. 320«ß‘™ B. 360«ß‘™ C. 400«ß‘™ D. 440«ß‘™
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄ƒ≥«¯°∞¥¥Œƒ√˜≥««¯°±£®ºÚ≥∆°∞¥¥≥«°±£©ªÓ∂Ø÷–£¨ΩÃŒØ∂‘±æ«¯![]() ÀƒÀ˘∏þ÷–—ß–£∞¥∏˜–£»À ˝∑÷≤„≥È—˘£¨Àʪ˙≥È≤È¡À100»À£¨Ω´µ˜≤È«ÈøˆΩ¯––’˚¿Ì∫Û÷∆≥…œ¬±Ì£∫
ÀƒÀ˘∏þ÷–—ß–£∞¥∏˜–£»À ˝∑÷≤„≥È—˘£¨Àʪ˙≥È≤È¡À100»À£¨Ω´µ˜≤È«ÈøˆΩ¯––’˚¿Ì∫Û÷∆≥…œ¬±Ì£∫
—ß–£ |
|
|
|
|
≥È≤È»À ˝ | 50 | 15 | 10 | 25 |
°∞¥¥≥«°±ªÓ∂Ø÷–≤Œ”僻À ˝ | 40 | 10 | 9 | 15 |
£®◊¢£∫≤Œ”ά «÷∏£∫“ªÀ˘—ß–£°∞¥¥≥«°±ªÓ∂Ø÷–≤Œ”僻À ˝”αª≥È≤È»À ˝µƒ±»÷µ£©ºŸ…Ë√ø√˚∏þ÷–—ß…˙ «∑Ò≤Œ”ΰ±¥¥≥«°±ªÓ∂Ø «œýª•∂¿¡¢µƒ.
£®1£©»Ù∏√«¯π≤2000√˚∏þ÷–—ß…˙£¨π¿º∆![]() —ß–£≤Œ”ΰ∞¥¥≥«°±ªÓ∂صƒ»À ˝£ª
—ß–£≤Œ”ΰ∞¥¥≥«°±ªÓ∂صƒ»À ˝£ª
£®2£©‘⁄Àʪ˙≥È≤ȵƒ100√˚∏þ÷–—ß…˙÷–£¨Àʪ˙≥È»°1√˚—ß…˙£¨«Û«°∫√∏√…˙√ª”–≤Œ”ΰ∞¥¥≥«°±ªÓ∂صƒ∏≈¬ £ª
£®3£©‘⁄…œ±Ì÷–¥”![]() ¡Ω–£√ª”–≤Œ”ΰ∞¥¥≥«°±ªÓ∂صƒÕ¨—ß÷–Àʪ˙≥È»°2»À£¨«Û«°∫√
¡Ω–£√ª”–≤Œ”ΰ∞¥¥≥«°±ªÓ∂صƒÕ¨—ß÷–Àʪ˙≥È»°2»À£¨«Û«°∫√![]() ¡Ω–£∏˜”–1»À√ª”–≤Œ”ΰ∞¥¥≥«°±ªÓ∂صƒ∏≈¬ «∂ý…Ÿ£ø
¡Ω–£∏˜”–1»À√ª”–≤Œ”ΰ∞¥¥≥«°±ªÓ∂صƒ∏≈¬ «∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂![]() ÷–£¨
÷–£¨ ![]() «µ»±þ»˝Ω«–Œ£¨
«µ»±þ»˝Ω«–Œ£¨ ![]() Œ™
Œ™![]() µƒ÷–µ„£¨Àƒ±þ–Œ
µƒ÷–µ„£¨Àƒ±þ–Œ![]() Œ™÷±Ω«Ã𖌣¨
Œ™÷±Ω«Ã𖌣¨ ![]()
![]()
![]()
![]() .
.
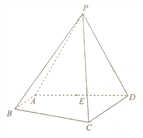
£®1£©«Û÷§£∫∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©«ÛÀƒ¿‚◊∂![]() µƒÃª˝£ª
µƒÃª˝£ª
£®3£©‘⁄¿‚![]() …œ «∑ҥʑ⁄µ„
…œ «∑ҥʑ⁄µ„![]() £¨ πµ√
£¨ πµ√![]() ∆Ω√Ê
∆Ω√Ê![]() £øÀµ√˜¿Ì”….
£øÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() .
.
£®¢Ò£©«Û«˙œþ![]() ‘⁄µ„
‘⁄µ„![]() ¥¶µƒ«–œþ∑Ω≥ãª
¥¶µƒ«–œþ∑Ω≥ãª
£®¢Ú£©«Û![]() µƒµ•µ˜«¯º‰£ª
µƒµ•µ˜«¯º‰£ª
£®¢Û£©»Ù∂‘”⁄»Œ“‚![]() £¨∂º”–
£¨∂º”–![]() £¨«Û µ ˝
£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
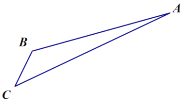
°æƒø°ø»ÁÕº£¨”ŒøÕ¥”ƒ≥¬√”Œæ∞«¯µƒæ∞µ„A¥¶œ¬…Ω÷¡C¥¶”–¡Ω÷÷¬∑æ∂.“ª÷÷ «¥”A—ÿ÷±œþ≤Ω––µΩC£¨¡Ì“ª÷÷ «œ»¥”A—ÿÀ˜µ¿≥À¿¬≥µµΩB£¨»ª∫Û¥”B—ÿ÷±œþ≤Ω––µΩC.œ÷”–º◊°¢““¡ΩŒª”ŒøÕ¥”A¥¶œ¬…Ω£¨º◊—ÿAC‘»ÀŸ≤Ω––£¨ÀŸ∂»Œ™![]() .‘⁄º◊≥ˆ∑¢
.‘⁄º◊≥ˆ∑¢![]() ∫Û£¨““¥”A≥À¿¬≥µµΩB£¨‘⁄B¥¶Õ£¡Ù
∫Û£¨““¥”A≥À¿¬≥µµΩB£¨‘⁄B¥¶Õ£¡Ù![]() ∫Û£¨‘Ÿ¥”B‘»ÀŸ≤Ω––µΩC.ºŸ…Ë¿¬≥µ‘»ÀŸ÷±œþ‘À∂صƒÀŸ∂»Œ™
∫Û£¨‘Ÿ¥”B‘»ÀŸ≤Ω––µΩC.ºŸ…Ë¿¬≥µ‘»ÀŸ÷±œþ‘À∂صƒÀŸ∂»Œ™![]() £¨…Ω¬∑AC≥§Œ™
£¨…Ω¬∑AC≥§Œ™![]() £¨æ≠≤‚¡ø£¨
£¨æ≠≤‚¡ø£¨![]() £¨
£¨![]() .µ±““≥ˆ∑¢________∑÷÷” ±£¨““‘⁄¿¬≥µ…œ”κ◊µƒæý¿Î◊Ó∂Ã.
.µ±““≥ˆ∑¢________∑÷÷” ±£¨““‘⁄¿¬≥µ…œ”κ◊µƒæý¿Î◊Ó∂Ã.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë’˝œÓ ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨«“¬˙◊„£∫
£¨«“¬˙◊„£∫![]() £¨
£¨![]() £¨
£¨![]() £Æ
£Æ
£®¢Ò£©«Û ˝¡–![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
£®¢Ú£©»Ù’˝œÓµ»±» ˝¡–![]() ¬˙◊„
¬˙◊„![]() £¨
£¨![]() £¨«“
£¨«“![]() £¨ ˝¡–
£¨ ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨»Ù∂‘»Œ“‚
£¨»Ù∂‘»Œ“‚![]() £¨æ˘”–
£¨æ˘”–![]() ∫„≥…¡¢£¨«Û µ ˝
∫„≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∑øµÿ≤˙ø™∑¢…ÃÕ∂◊ 81ÕÚ‘™Ω®“ª◊˘–¥◊÷¬•£¨µ⁄“ªƒÍ◊∞–ÞŒ¨ª§∑—Œ™1ÕÚ‘™£¨“‘∫Û√øƒÍ‘ˆº”2ÕÚ‘™£¨∞—–¥◊÷¬•≥ˆ◊‚£¨√øƒÍ ’»Î◊‚Ω30ÕÚ‘™.
£®1£©»Ùø€≥˝Õ∂◊ ∫Õ∏˜÷÷◊∞–ÞŒ¨ª§∑—£¨‘Ú¥”µ⁄º∏ƒÍø™ ºªÒ»°¥ø¿˚»Û£ø
£®2£©»Ù∏…ƒÍ∫Ûø™∑¢…ÃŒ™¡ÀÕ∂◊ ∆‰À˚œÓƒø£¨”–¡Ω÷÷¥¶¿Ì∑Ω∞∏£∫¢Ÿ¥ø¿˚»Û◊Ð∫Õ◊Ó¥Û ±£¨“‘10ÕÚ‘™≥ˆ €∏√¬•£ª¢⁄ƒÍ∆Ωæ˘¿˚»Û◊Ó¥Û ±“‘46ÕÚ‘™≥ˆ €∏√¬•£¨Œ ƒƒ÷÷∑Ω∞∏∏¸”≈£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™‘⁄÷±Ω«Ãð–Œ![]() ÷–£¨
÷–£¨ ![]() £¨
£¨ ![]() £¨Ω´
£¨Ω´![]() —ÿ
—ÿ![]() ’€∆÷¡
’€∆÷¡![]() £¨ π∂˛√ÊΩ«
£¨ π∂˛√ÊΩ«![]() Œ™÷±Ω«.
Œ™÷±Ω«.
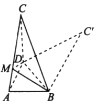
(1)«Û÷§£∫∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
(2)»Ùµ„![]() ¬˙◊„
¬˙◊„![]() ,
, ![]() £¨µ±∂˛√ÊΩ«
£¨µ±∂˛√ÊΩ«![]() Œ™45°„ ±£¨«Û
Œ™45°„ ±£¨«Û![]() µƒ÷µ.
µƒ÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com