
【题目】直线![]() 与双曲线
与双曲线![]() 的渐近线交于
的渐近线交于![]() 两点,设
两点,设![]() 为双曲线上任一点,若
为双曲线上任一点,若![]() 为坐标原点),则下列不等式恒成立的是( )
为坐标原点),则下列不等式恒成立的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知与曲线![]() 相切的直线
相切的直线![]() ,与
,与![]() 轴,
轴, ![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为原点,
为原点, ![]() ,
, ![]() ,(
,( ![]() ).
).
(1)求证:: ![]() 与
与![]() 相切的条件是:
相切的条件是: ![]() .
.
(2)求线段![]() 中点的轨迹方程;
中点的轨迹方程;
(3)求三角形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求函数y=f(x)的解析式,并用“五点法作图”在给出的直角坐标系中画出函数y=f(x)在区间[0,π]上的图象; 
(2)设α∈(0,π),f( ![]() )=
)= ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Sn为数列{an}的前n项和,已知an>0,an2+2an=4Sn+3
(I)求{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于f(x)=4sin![]() (x∈R),有下列命题
(x∈R),有下列命题
①由f(x1)=f(x2)=0可得x1-x2是π的整数倍;
②y=f(x)的表达式可改写成y=4cos![]() ;
;
③y=f(x)图象关于![]() 对称;
对称;
④y=f(x)图象关于x=-![]() 对称.
对称.
其中正确命题的序号为________(将你认为正确的都填上)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在印度有一个古老的传说:舍罕王打算奖赏国际象棋的发明人——宰相宰相西萨班达依尔.国王问他想要什么,他对国王说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍.请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!”国王觉得这要求太容易满足了,就命令给他这些麦粒.当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求.那么,宰相要求得到的麦粒到底有多少粒?下面是四位同学为了计算上面这个问题而设计的程序框图,其中正确的是( )
A. 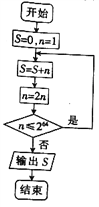 B.
B.  C.
C.  D.
D. 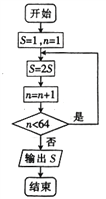
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( ) 
A.31.2
B.32.4
C.33.6
D.34.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com