
分析 (Ⅰ)令$\frac{α+β}{2}=x,\frac{α-β}{2}=y$,得α=x+y,β=x-y,代入$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{2}$-cosβ后可得$-2(cosx-\frac{cosy}{2})^{2}+\frac{co{s}^{2}y}{2}$=$\frac{1}{2}$,由三角函数的有界性得到cosx=$\frac{1}{2}$,cosy=1,由此求得x,y的值,进一步得到α、β的值,再代入数量积求夹角公式求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ;
(Ⅱ)直接由(Ⅰ)中得答案.
解答 解:(Ⅰ)令$\frac{α+β}{2}=x,\frac{α-β}{2}=y$,则 α+β=2x,α-β=2y,
α=x+y,β=x-y,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=cosα-cosαcosβ+sinαsinβ=cosα-cos(α+β),
由$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{2}$-cosβ,整理可得2cosxcosy-2cos2x=$\frac{1}{2}$,
但2cosxcosy-2cos2x=$-2(cosx-\frac{cosy}{2})^{2}+\frac{co{s}^{2}y}{2}$,
∴$-2(cosx-\frac{cosy}{2})^{2}+\frac{co{s}^{2}y}{2}$=$\frac{1}{2}$,
∵$-2(cosx-\frac{cosy}{2})^{2}≤0$,而 cos2y≤1,
∴$-2(cosx-\frac{cosy}{2})^{2}+\frac{co{s}^{2}y}{2}$≤$\frac{1}{2}$,
∴最大值被达到时,有cosx-$\frac{cosy}{2}=0$,cosy=1,
即cosx=$\frac{1}{2}$,cosy=1,
而0<α,β<π,∴0<x<π,-$\frac{π}{2}$<y<$\frac{π}{2}$,
∴x=$\frac{π}{3}$,y=0,
可得:α=β=$\frac{π}{3}$,
∴$\overrightarrow{a}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$),$\overrightarrow{b}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$),
则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{\frac{1}{4}+\frac{3}{4}}{1×1}=1$,
即θ=0;
(Ⅱ)由(Ⅰ)可知α=β=$\frac{π}{3}$.
点评 本题考查平面向量的数量积运算,考查学生的灵活变形能力和逻辑思维能力,而令$\frac{α+β}{2}=x,\frac{α-β}{2}=y$进行转化运算是该题的难点所在,该题属难度较大的题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | $(-\frac{1}{2},+∞)$ | C. | (0,1) | D. | $(-\frac{1}{2},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
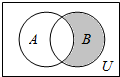 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )| A. | {3} | B. | {-2} | C. | {3,-2} | D. | {∅} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com