练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    一般来说，一个人脚掌越长，他的身高就越高，现对10名成年人的脚掌长与身高进行测量，得到数据（单位均为）如表，作出散点图后，发现散点在一条直线附近，经计算得到一些数据：，；某刑侦人员在某案发现场发现一对裸脚印，量得每个脚印长为，则估计案发嫌疑人的身高为
        ．
    脚长
    		20
    		21
    		22
    		23
    		24
    		25
    		26
    		27
    		28
    		29
    身高
    		141
    		146
    		154
    		160
    		169
    		176
    		181
    		188
    		197
    		203
    185.5

    试题分析：回归方程的斜率，，，截距，即回归方程为，当，，
    点评：回归直线方程过样本点中心，这条性质要牢固掌握，灵活应用.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本题12分）为了研究化肥对小麦产量的影响，某科学家将一片土地划分成200个的小块，并在100个小块上施用新化肥，留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位：kg)
    表1：施用新化肥小麦产量频数分布表
    小麦产量





    频数
    		10
    		35
    		40
    		10
    		5
    表2：不施用新化肥小麦产量频数分布表
    小麦产量




    频数
    		15
    		50
    		30
    		5
    (10)     完成下面频率分布直方图；

    (2)统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量；
    (3)完成下面2×2列联表，并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
    表3：
     
    		小麦产量小于20kg
    		小麦产量不小于20kg
    		合计
    施用新化肥


    		 
    不施用新化肥


    		 
    合计
    		 
    		 

     
    附：

    		0.050
    		0.010
    		0.005
    		0.001

    		3.841
    		6.635
    		7.879
    		10.828
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    正定中学教学处采用系统抽样方法，从学校高三年级全体800名学生中抽50名学生做学习状况问卷调查。现将800名学生从1到800进行编号，在中随机抽取一个数，如果抽到的是7，则从中应取的数是         

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成6组后，得到部分频率分布直方图（如图），观察图中的信息，回答下列问题．

    (Ⅰ)求分数在[70，80）内的频率，并补全这个频率分布直方图；
    (Ⅱ)根据频率分布直方图，估计本次考试的平均分；
    (Ⅲ)若从60名学生中随机抽取2人，抽到的学生成绩在[40，70）记0分，记[70，100]记1分，用X表示抽取结束后的总记分，求X的分布列和数学期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在对某样本进行实验时，测得如下数据：则与之间的回归直线方程为（　　）

    		2
    		1
    		4
    		3

    		3
    		2
    		5
    		4
    A、　　　B、　　　C、　　　D、

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    一组数据，，，，的极差是7，那么的值是           .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    随机抽取某中学甲、乙两面个班10名同学，测量他们的身高（单位：cm）后获得身高数据的茎叶图如图甲所示，在这20人中，记身高在内的人数依次为，图乙是统计样本中身高在一定范围内的人数的算法流程图，则下列说法正确的是（  ）
     
    A．由图甲可知甲、乙两班中身高的中位数较大的是甲班，图乙输出的S的值为18
    B．由图甲可知甲、乙两班中身高的中位数较大的是乙班，图乙输出的S的值为18
    C．由图甲可知甲、乙两班中身高的中位数较大的是乙班，图乙输出的S的值为16
    D．由图甲可知甲、乙两班中身高的中位数较大的是甲班，图乙输出的S的值为16

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    某大学高等数学老师上学期分别采用了两种不同的教学方式对甲、乙两个大一新生班进行教改试验（两个班人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩，得到茎叶图如下：

    （Ⅰ）依茎叶图判断哪个班的平均分高？
    （Ⅱ）从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学，求成绩为90分的同学被抽中的概率；
    （Ⅲ）学校规定：成绩不低于85分的为优秀，请填写下面的列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”
     
    		甲班
    		乙班
    		合计
    优秀
    		 
    		 
    		 
    不优秀
    		 
    		 
    		 
    合计
    		 
    		 
    		 
    下面临界值表仅供参考：

    		0.15
    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001

    		2.072
    		2.706
    		3.841
    		5.024
    		6.635
    		7.879
    		10.828
    （参考公式：其中） 
    （Ⅳ）从乙班高等数学成绩不低于85分的同学中抽取2人，成绩不低于90分的同学得奖金100元，否则得奖金50元，记为这2人所得的总奖金，求的分布列和数学期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分13分)
    甲、乙两台机床生产同一型号零件．记生产的零件的尺寸为(cm)，相关行业质检部门规定：若，则该零件为优等品；若，则该零件为中等品；其余零件为次品．现分别从甲、乙机床生产的零件中各随机抽取50件，经质量检测得到下表数据：
    尺寸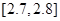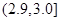






    甲机床零件频数
    		2
    		3
    		20
    		20
    		4
    		1
    乙机床零件频数
    		3
    		5
    		17
    		13
    		8
    		4
    （Ⅰ）设生产每件产品的利润为：优等品3元，中等品1元，次品亏本1元. 若将频率视为概率，试根据样本估计总体的思想，估算甲机床生产一件零件的利润的数学期望；
    （Ⅱ）对于这两台机床生产的零件，在排除其它因素影响的情况下，试根据样本估计总体的思想，估计约有多大的把握认为“零件优等与否和所用机床有关”，并说明理由.
    参考公式：.
    参考数据：

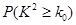    		0．25
    		0．15
    		0．10
    		0．05
    		0．025
    		0.010

    		1．323
    		2．072
    		2．706
    		3．841
    		5．024
    		6.635
     

    查看答案和解析>>

    同步练习册答案