练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在海岛O上有一座海拔1千米的山，山顶设有一个观察站A，上午11时，测得一轮船在岛北60°东，俯角为30°的C处，到11时10分，又测得该船在岛北60°西，俯角为60°的B处，（如图）．求：

    （1）船的航行速度；

    （2）又经过一段时间后，船到达海岛O的正西方向的E处，问此时船距岛O有多远?

    答案：
    解析：

    		解（1）由已知，在RtDABO中，OB=OA×cot60°=(km)；在DACO中，

    OC=OA×cot30°=(km)；在DBOC中，由余弦定理得

    BC2=OB2+OC2-2×OB×OC×cosÐBOC=+3-2´cos120°=．

    ∴ BC=(km)，∵ 船从C行到B用去10min=h，

    ∴ 船速

    （2）在DBOC中，由余弦定理得，sinÐOBC=

    ∴ sinÐBEO=sin[180°-(30°+ÐEBO)]

    =(30°+ÐEBO)

    =

    在DBOE中，由正弦定理得，

    ∴ BE=(km)

    于是从B至E所需时间．

    此时

    ∴ 船在11时15分到达海岛正西方向，此时点E离开工海岛1.5km．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

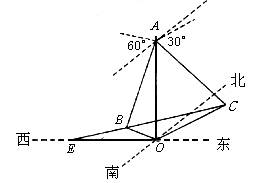
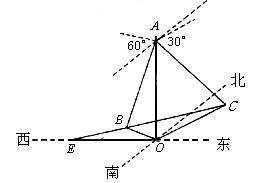
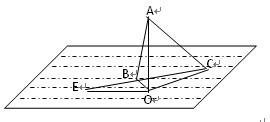
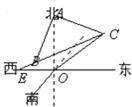    精英家教网海岛O上有一座海拔1000米的山，山顶上设有一个观察站A，上午11时，测得一轮船在岛北偏东60°C处，俯角30°，11时10分，又测得该船在岛的北偏西60°西B处，俯角60°．
    ①这船的速度每小时多少千米？
    ②如果船的航速不变，它何时到达岛的正西方向？此时所在点E离岛多少千米？

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    在海岛O上有一座海拔1千米的山，山顶设有一个观察站A，上午11时，测得一轮船在岛北60°东，俯角为30°的C处，到11时10分，又测得该船在岛北60°西，俯角为60°的B处，（如图）．求：

    （1）船的航行速度；

    （2）又经过一段时间后，船到达海岛O的正西方向的E处，问此时船距岛O有多远?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    素材1：上午11时测得一轮船在海岛O北偏东60°的C处，俯角为30°；

    素材2：海岛O上有一座海拔1 000 m高的山，山顶上设有一个观察站A；

    素材3：上午11时30分测得轮船在岛的北偏西60°的B处，俯角为60°.

    将上面的素材构建成一个问题，然后再解答.

    查看答案和解析>>

    科目：高中数学 来源：2012年人教B版高中数学必修5 1.2应用举例练习卷（解析版） 题型：解答题

     海岛O上有一座海拔1000m的山，山顶上设有一个观察站A，上午11时测得一轮船在岛北偏东60o的C处，俯角为30o，11时10分又测得该船在岛北偏西60o的B处，俯角为60o，如图所示，求：

    （1）该船的速度为每小时多少千米？

    （2）若此船以匀速度继续航行，则它何时到达岛的正西方向？此时，船所在点E离开海岛多少千米？

     

    查看答案和解析>>

    同步练习册答案