
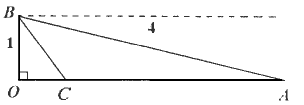
如下图,一条河宽1km,相距4km(直线距离)的两座城市,A,B分别位于河的两岸(假定岸是平行的直线),现需铺设一条电缆连通A与B,已知地下电缆的修建费为每千米2万元,水下电缆的修建费为每千米4万元,问应如何铺设电缆可使总的修建费用最少?(![]() =1.732,
=1.732,![]() =2.236,
=2.236,![]() =3.8730)
=3.8730)
|
思路 本例的关键在于确定水中电缆的长度,即C点位置.由于选择参变数的不同,总的修建费的目标函数的表达方式各异,因而有判别式法、平均值不等式法、三角换元法、平面几何作图法等不同解法. 解答 解法一 设C为OA上一点,OC=x(km), 则CA= ∴总修建费y=2( 12x2+(8 ∵△=(8 =y2-4 ∴y≥2 2 即3x2-2 即当x= 此时CA≈3.3(km),BC≈1.2(km). 答:先沿岸边铺设3.3km的地下电缆,再铺设1.2km水下电缆连通A,B两市时,总修建费最少. 解法二 设C为OA上一点, ∠OBC=α,α∈(0,arccos 则BC= ∴总修建费y=2( =2 则sinα+tcosα=2, ∴sin(α+ 由|sin(α+ ∴y≥2 当t= 解之得x= 此时CA= BC= 解法三 如下图,作∠DAO=
因为水下电缆修建费是地下电缆修建费的2倍,所以A 而B到直线AD的最短距离为垂线段BF,所以A ∴OC= 此时AC≈3.3(km),BC≈1.2(km) 评析 解法一叫做判别式法,在用判别式法求函数最值时应注意最值是否能真正取到,即是否存在与最值相应的自变量值,也就是“△≥0”的“=”能否成立.简单地说是应验证.解法三是平面几何作图法,形象直观,但必须叙述、推理严谨. |


科目:高中数学 来源: 题型:044
如图,一条河宽1km,两岸各有城市A与B,其直线距离为4km,今需铺设一条电缆连结A与B,已知地下电缆的修建费为2万元/km,水下电缆的修建费是4万元/km,假定河两岸是平行直线,问应如何架设电缆方可使总施工费用最少?

查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
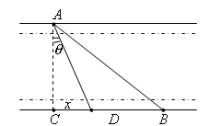
如下图,一条河宽1千米,相距4千米(直线距离)的两座城市A和B,分别位于河的两岸(城市A,B与岸的距离忽略不计).现需铺设一条电缆连通城市A与B.已知水下电缆的修建费为4万元/千米,地下电缆的修建费为2万元/千米,假设两岸是平行直线,问:应如何铺设电缆可使总费用最少?(![]() =3.873,
=3.873,![]() =1.732,精确到百米,百元)
=1.732,精确到百米,百元)

查看答案和解析>>
科目:高中数学 来源:学习高手必修四数学苏教版 苏教版 题型:044
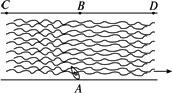
如下图,一条河的两岸平行,河宽为500米,一艘船从A处出发到对岸,船速为10千米/时,水流速度为2千米/时.求航程最短时,船到达对岸所用的时间.(精确到0.1分钟)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com