
分析 (Ⅰ)本题是一个古典概型,由分步计数原理知基本事件共6个,当a>0,b>0时,方程x2+2ax+b2=0有实根的充要条件为a≥b,满足条件的事件中包含1个基本事件,由古典概型公式得到结果.
(Ⅱ)本题是一个几何概型,试验的全部约束所构成的区域为{(a,b)|1≤a≤3,1≤b≤2}.构成事件A的区域为{(a,b)|1≤a≤3,1≤b≤2,a≥b}.根据几何概型公式得到结果.
解答 解:(Ⅰ)基本事件共3×2=6个:(1,1),(1,2),(2,1),(2,2),(3,1),(3,2)
当a>0,b>0时,方程x2+2ax+b2=0有实根的充要条件为a≥b,方程在(-4,0)内有两个不等实根的基本事件有(2,1)
∴所求概率为$\frac{1}{6}$;
(Ⅱ)设事件A为“方程a2+2ax+b2=0有实根”.
当a>0,b>0时,方程x2+2ax+b2=0有实根的充要条件为a≥b.
试验的全部约束所构成的区域为{(a,b)|1≤a≤3,1≤b≤2}.
构成事件A的区域为{(a,b)|1≤a≤3,1≤b≤2,a≥b}.
所以所求的概率为=$\frac{2×2-\frac{1}{2}×(1+2)×1}{2×2}$=$\frac{5}{8}$.
点评 本题考查几何概型和古典概型,放在一起的目的是把两种概型加以比较,几何概型和古典概型是高中必修中学习的高考时常以选择和填空出现,有时文科会考这种类型的解答题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
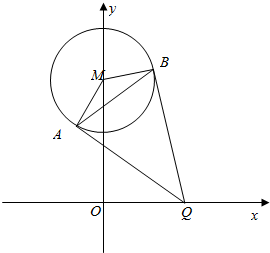 如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.
如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,5) | B. | (0,-5) | C. | (5,0) | D. | (-5,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com