
 使得数列
使得数列 满足:若
满足:若 是数列
是数列 中的一项,则
中的一项,则 也是数列
也是数列 中的一项,称数列
中的一项,称数列 为“兑换数列”,常数
为“兑换数列”,常数 是它的“兑换系数”.
是它的“兑换系数”. 是“兑换系数”为
是“兑换系数”为 的“兑换数列”,求
的“兑换数列”,求 和
和 的值;
的值; 的项数是
的项数是 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列 是“兑换数列”,并用
是“兑换数列”,并用 和
和 表示它的“兑换系数”;
表示它的“兑换系数”; ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.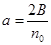
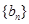 的公差为d,因为数列
的公差为d,因为数列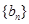 是项数为
是项数为 项的有穷等差数列
项的有穷等差数列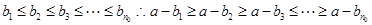
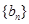 中的任意一项
中的任意一项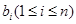
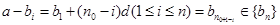 -------------------6分
-------------------6分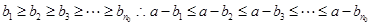 ,
,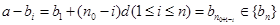 也成立,
也成立,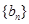 是 “兑换数列”;-------------------8分
是 “兑换数列”;-------------------8分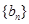 所有项之和是B,所以
所有项之和是B,所以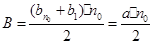 ,即
,即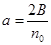 ------10分
------10分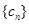 ,设它的公比为q,(q>1),
,设它的公比为q,(q>1),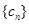 为递增数列,所以
为递增数列,所以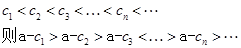
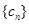 为“兑换数列”,则
为“兑换数列”,则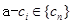 ,所以
,所以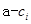 是正整数
是正整数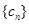 必为有穷数列,不妨设项数为n项,------------------12分
必为有穷数列,不妨设项数为n项,------------------12分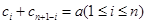 ----------14分
----------14分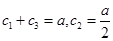 ,又
,又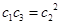 ,由此得q=1,与q>1矛盾;-------------------15分
,由此得q=1,与q>1矛盾;-------------------15分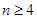 。由
。由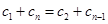 ,
, 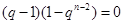 ),故q=1,与q>1矛盾;-------------------17分
),故q=1,与q>1矛盾;-------------------17分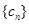 。-------------------18分
。-------------------18分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com