
在平面直角坐标系中,O为坐标原点,给定两点A(1,0),B(0,﹣2),点C满足![]() ,其中m,n∈R且m﹣2n=1.
,其中m,n∈R且m﹣2n=1.
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线![]() (a>0,b>0且a≠b)交于M、N两点,且以MN为直径的圆过原点,求证:
(a>0,b>0且a≠b)交于M、N两点,且以MN为直径的圆过原点,求证:![]() 为定值;
为定值;
(3)在(2)的条件下,若双曲线的离心率不大于![]() ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
考点:
直线与圆锥曲线的综合问题;轨迹方程;双曲线的简单性质.
专题:
计算题.
分析:
(1)由向量等式,得点C的坐标,消去参数即得点C的轨迹方程;
(2)将直线与双曲线方程组成方程组,利用方程思想,求出x1x2+y1y2,再结合向量的垂直关系得到关于a,b的关系,化简即得结论.
(3)由(2)得![]() 从而
从而![]() 又e
又e![]() 得出
得出![]() .解得双曲线实轴长2a的取值范围即可.
.解得双曲线实轴长2a的取值范围即可.
解答:
解:(1)设C(x,y),∵![]()
∴(x,y)=m(1,0)+n(0,﹣2).
∴![]() ∵m﹣2n=1,
∵m﹣2n=1,
∴x+y=1
即点C的轨迹方程为x+y=1(15分)
(2)由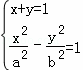 得(b2﹣a2)x2+2a2x2﹣a2﹣a2b2=0
得(b2﹣a2)x2+2a2x2﹣a2﹣a2b2=0
由题意得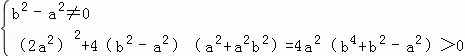 (8分)
(8分)
设M(x1,y1),N(x2,y2),
则 ![]()
∵以MN为直径的圆过原点,∴![]() .即x1x2+y1y2=0.
.即x1x2+y1y2=0.
∴x1x2+(1﹣x1)(1﹣x2)=1﹣(x1+x2)+2x1x2=![]() .即b2﹣a2﹣2a2b2=0.
.即b2﹣a2﹣2a2b2=0.
∴![]() 为定值.(14分)
为定值.(14分)
(3)∵![]()
∴![]()
∵e![]() ∴
∴![]() .
.
∴![]()
解得:0<a≤![]() ,0<2a≤1
,0<2a≤1
∴双曲线实轴长的取值范围是(0,1].
点评:
本小题主要考查双曲线的标准方程和几何性质、直线方程、求曲线的方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com