
【题目】某班有两个课外活动小组,其中第一小组有足球票6张,排球票4张;第二个小组有
足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,乙从第二小组的10
张票中任抽1张.
(1)两人都抽到足球票的概率是多少?
(2)两人中至少有一人抽到足球票的概率是多少?
【答案】(Ⅰ) 两人都抽到足球票的概率是![]()
(Ⅱ)两人中至少有1人抽到足球票的概率是![]()
【解析】记“甲从第一小组的10张票中任抽1张,抽到足球票”为事件A,“乙从第二小组的10张票中任抽1张,抽到足球票”为事件B,则“甲从第一小组的10张票中任抽1张,抽到排球票”为事件![]() ,“乙从第二小组的10张票中任抽1张,抽到排球票”为事件
,“乙从第二小组的10张票中任抽1张,抽到排球票”为事件![]() ,
,
2分
于是![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
由于甲(或乙)是否抽到足球票,对乙(或甲)是否抽到足球票没有影响,因此A与B是相互独立事件. 6分
(Ⅰ)甲、乙两人都抽到足球票就是事件A·B发生,根据相互独立事件的概率乘法公式,得到
P(A·B)=P(A)·P(B)=![]() =
=![]() .
.
答:两人都抽到足球票的概率是![]() . 9分
. 9分
(Ⅱ)甲、乙两人均未抽到足球票(事件![]() ·
·![]() 发生)的概率为:
发生)的概率为:
P(![]() ·
·![]() )=P(
)=P(![]() )·P(
)·P(![]() )=
)=![]() =
=![]() .
.
∴ 两人中至少有1人抽到足球票的概率为:
P=1-P(![]() ·
·![]() )=1-
)=1-![]() =
=![]() . 11分
. 11分
答:两人中至少有1人抽到足球票的概率是![]() . 12分
. 12分


科目:高中数学 来源: 题型:
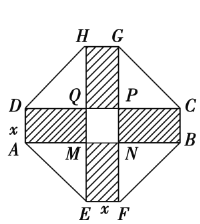
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地
区调查了500位老年人,结果如下:
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否在犯错误的概率不超过0.01的前提下认为该地区的老年人需要志愿者提供帮助与性别有
关?
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台. 现销售给A地10台,B地8台. 已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的费用分别为300元和500元.
(1)设从甲地调运x台至A地,求总费用y关于台数x的函数解析式;
(2)若总运费不超过9 000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=2.
(1)求函数f(x)和g(x);
(2)判断函数f(x)+g(x)的奇偶性;
(3)求函数f(x)+g(x)在(0,![]() ]上的最小值.
]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2-2ax+2+b(a≠0)在区间[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-2mx在[2,4]上单调,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com