
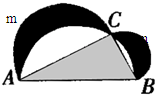
 如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( ) 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
 如图,已知△ABC为正三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、BD在平面ABC的同侧,M为EA的中点,CE=CA=2BD,求证:
如图,已知△ABC为正三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、BD在平面ABC的同侧,M为EA的中点,CE=CA=2BD,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
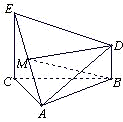 如图,已知△ABC为正三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、BD在平面ABC的同侧,M为EA的中点,CE=CA=2BD,
如图,已知△ABC为正三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、BD在平面ABC的同侧,M为EA的中点,CE=CA=2BD,查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:7 立体几何 质量检测(1)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com