
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,若(2a﹣c)cosB=bcosC.
(1)求角B的大小,
(2)若a=3,△ABC的面积为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:∵(2a﹣c)cosB=bcosC,
由正弦定理得:(2sinA﹣sinC)cosB=sinBcosC,
∴2sinAcosB=sinCcosB+cosCsinB=sin(B+C)=sinA,
∵0<A<π,∴sinA>0,∴2cosB=1,cosB= ![]() ,
,
又0<B<π,∴B= ![]()
(2)解:法一:∵a=3,△ABC的面积为 ![]() ,
,
∴ ![]() 3csin
3csin ![]() =
= ![]() ,
,
∴c=2,
b2=22+32﹣2×2×3cos ![]() =7,
=7,
∴b= ![]() ,
,
∴cosA= ![]() =
= ![]() ,
,
∴ ![]()
![]() =bccos(π﹣A)=2
=bccos(π﹣A)=2 ![]() ×(﹣
×(﹣ ![]() )=﹣1.
)=﹣1.
法二: ![]()
![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() )
)
=| ![]() ||
|| ![]() |cos<
|cos< ![]() ,
, ![]() >﹣
>﹣ ![]()
=2×3× ![]() ﹣22=﹣1
﹣22=﹣1
【解析】(Ⅰ)运用正弦定理和两角和的正弦公式,简整理,即可得到B;(Ⅱ)运用三角形的面积公式和余弦定理,结合向量的数量积的定义,即可计算得到.


科目:高中数学 来源: 题型:
【题目】如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1 , y1),B(x2 , y2)均在抛物线上. 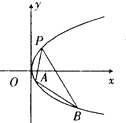
(1)求该抛物线方程;
(2)若AB的中点坐标为(1,﹣1),求直线AB方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)经过点(1,
(a>b>0)经过点(1, ![]() ),且离心率等于
),且离心率等于 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)过点P(2,0)作直线PA,PB交椭圆于A,B两点,且满足PA⊥PB,试判断直线AB是否过定点,若过定点求出点坐标,若不过定点请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域是一切实数的函数y=f(x),其图象是连续不断的,且存在常数λ(λ∈R)使得f(x+λ)+λf(x)=0对任意实数x都成立,则称f(x)实数一个“λ一半随函数”,有下列关于“λ一半随函数”的结论:①若f(x)为“1一半随函数”,则f(0)=f(2);②存在a∈(1,+∞)使得f(x)=ax为一个“λ一半随函数;③“ ![]() 一半随函数”至少有一个零点;④f(x)=x2是一个“λ一班随函数”;其中正确的结论的个数是( )
一半随函数”至少有一个零点;④f(x)=x2是一个“λ一班随函数”;其中正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条直线l1:2x+y﹣2=0与l2:2x﹣my+4=0.
(1)若直线l1⊥l2 , 求直线l1与l2交点P的坐标;
(2)若l1 , l2以及x轴围成三角形的面积为1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点是A(4,0),B(6,7),C(0,3).
(1)求过点A与BC平行的直线方程.
(2)求过点B,并且在两个坐标轴上截距相等的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com