
【题目】设抛物线![]() ,点
,点![]() ,
, ![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)当![]() 与
与![]() 轴垂直时,求直线
轴垂直时,求直线![]() 的方程;
的方程;
(2)证明: ![]() .
.
【答案】(1) y=![]() 或
或![]() .
.
(2)见解析.
【解析】分析:(1)首先根据![]() 与
与![]() 轴垂直,且过点
轴垂直,且过点![]() ,求得直线l的方程为x=1,代入抛物线方程求得点M的坐标为
,求得直线l的方程为x=1,代入抛物线方程求得点M的坐标为![]() 或
或![]() ,利用两点式求得直线
,利用两点式求得直线![]() 的方程;
的方程;
(2)分直线l与x轴垂直、l与x轴不垂直两种情况证明,特殊情况比较简单,也比较直观,对于一般情况将角相等通过直线的斜率的关系来体现,从而证得结果.
详解:(1)当l与x轴垂直时,l的方程为x=2,可得M的坐标为(2,2)或(2,–2).
所以直线BM的方程为y=![]() 或
或![]() .
.
(2)当l与x轴垂直时,AB为MN的垂直平分线,所以∠ABM=∠ABN.
当l与x轴不垂直时,设l的方程为![]() ,M(x1,y1),N(x2,y2),则x1>0,x2>0.
,M(x1,y1),N(x2,y2),则x1>0,x2>0.
由![]() 得ky2–2y–4k=0,可知y1+y2=
得ky2–2y–4k=0,可知y1+y2=![]() ,y1y2=–4.
,y1y2=–4.
直线BM,BN的斜率之和为
![]() .①
.①
将![]() ,
, ![]() 及y1+y2,y1y2的表达式代入①式分子,可得
及y1+y2,y1y2的表达式代入①式分子,可得
![]() .
.
所以kBM+kBN=0,可知BM,BN的倾斜角互补,所以∠ABM=∠ABN.
综上,∠ABM=∠ABN.


科目:高中数学 来源: 题型:
【题目】先后掷一颗质地均匀的骰子(骰子的六个面上分别标有1,2,3,4,5,6)两次,落在水平桌面上后,记正面朝上的点数分别为![]() ,记事件
,记事件![]() 为“
为“![]() 为偶数”,事件
为偶数”,事件![]() 为“
为“![]() 中有偶数且
中有偶数且![]() ”,则概率
”,则概率![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若同时满足下列条件:
,若同时满足下列条件:
①![]() 在
在![]() 内单调递增或单调递减;
内单调递增或单调递减;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ;那么把
;那么把![]() (
(![]() )叫闭函数.
)叫闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)判断函数![]() 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=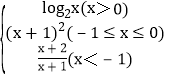 ,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,曲线
为奇函数,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,导函数
垂直,导函数![]() 的最小值为-12.
的最小值为-12.
(1)求函数![]() 的解析式;
的解析式;
(2)用列表法求函数![]() 在
在![]() 上的单调增区间、极值、最值.
上的单调增区间、极值、最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)= ,
,
(1)求实数m的值
(2)作出![]() 的图象,并指出当方程
的图象,并指出当方程![]() 只有一解,a的取值范围(不必写过程)
只有一解,a的取值范围(不必写过程)
(3)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com