
如图所示,已知椭圆方程为 ,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且
,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且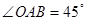 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )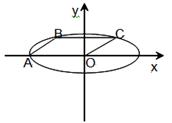
A、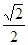 B、
B、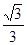 C、
C、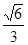 D、
D、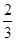
C
解析试题分析:令椭圆的右端点为M,连接CM,由题意四边形OABC为平行四边形,且∠OAB=45°,B,C在椭圆上,可得∠COM=∠CMO=∠OAB=45°,则有∠OCM=90°,故可得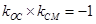 ,又四边形OABC为平行四边形,B,C在椭圆上,由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,故C的横坐标为
,又四边形OABC为平行四边形,B,C在椭圆上,由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,故C的横坐标为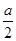 ,代入椭圆的方程得
,代入椭圆的方程得 得y=±
得y=± ,由图形知C(
,由图形知C(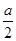 ,
, ),故有
),故有 ,∴
,∴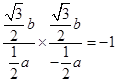 ,解得
,解得 ,故
,故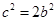 ,所以
,所以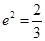
,得e=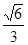
考点:本题考查椭圆的简单性质。
点评:求解本题的关键是根据椭圆的对称性得出点C的坐标以及图形中的垂直关系,求出点C的坐标是为了表示出斜率,求出垂直关系是为了利用斜率的乘积为-1建立方程,然后再根据求离心率的公式求出离心率即可.本题比较抽象,方法单一,入手较难,运算量不大.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com