
ЎҫМвДҝЎҝ2019ДкКАҪзәЈСуИХфЯИ«№ъәЈСуРыҙ«ИХЦчіЎ»о¶ҜФЪәЈДПИэСЗҫЩРРЈ¬ҙЛҙО»о¶ҜЦчМвОӘЎ°ХдП§әЈСуЧКФҙұЈ»ӨәЈСуЙъОп¶аСщРФЎұЈ¬ЦјФЪҪшТ»ІҪМбёЯ№«ЦЪ¶ФҪЪФјАыУГәЈСуЧКФҙ.ұЈ»ӨәЈСуЙъОп¶аСщРФөДИПК¶Ј¬ОӘұЈ»ӨА¶Й«јТФ°Чціц№ұПЧ.БӘәП№ъУЪөЪ63ҪмБӘәП№ъҙу»бЙПҪ«ГҝДкөД6ФВ8ИХИ·¶ЁОӘЎ°КАҪзәЈСуИХЎұЈ¬ОӘБЛПмУҰКАҪзәЈСуИХөД»о¶ҜЈ¬2019Дк12ФВұұҫ©ДіёЯРЈРРХюЦч№ЬІҝГЕҙУёГҙуС§Лж»ъійИЎІҝ·ЦҙуС§ЙъҪшРРТ»ҙОәЈСуЦӘК¶ІвКФЈ¬ІўёщҫЭұ»ІвСйС§ЙъөДіЙјЁЈЁөГ·Ц¶јФЪЗшјд![]() ДЪЈ©»жЦЖіЙИзНјЛщКҫөДЖөВК·ЦІјЦұ·ҪНј.
ДЪЈ©»жЦЖіЙИзНјЛщКҫөДЖөВК·ЦІјЦұ·ҪНј.
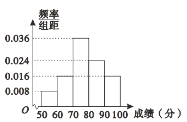
ИфС§ЙъөДөГ·ЦіЙјЁІ»өНУЪ80·ЦөДИПОӘКЗЎ°іЙјЁУЕРгЎұПЦФЪҙУИПОӘЎ°іЙјЁУЕРгЎұөДС§ЙъЦРёщҫЭФӯУР·ЦЧй°ҙХХ·ЦІгійСщөД·Ҫ·ЁійИЎ10ИЛҪшРРҪұАшЈ¬ЧоәуФЩҙУХв10ИЛЦРЛж»ъСЎИЎ3ИЛЧчОӘУЕРгҙъұн·ўСФ.
ЈЁ1Ј©ЗуЛщійИЎөД3ИЛІ»КфУЪН¬Т»ЧйөДёЕВКЈ»
ЈЁ2Ј©јЗХв3ИЛЦРЈ¬![]() ОӘІвКФіЙјЁФЪ
ОӘІвКФіЙјЁФЪ![]() ДЪөДИЛКэЈ¬Зу
ДЪөДИЛКэЈ¬Зу![]() өД·ЦІјБРәНКэС§ЖЪНы.
өД·ЦІјБРәНКэС§ЖЪНы.
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©·ЦІјБРјыҪвОцЈ¬1.2.
Ј»ЈЁ2Ј©·ЦІјБРјыҪвОцЈ¬1.2.
ЎҫҪвОцЎҝ
ЈЁ1Ј©ПИёщҫЭ·ЦІгійСщЗуіцБҪЧйөДИЛКэЈ¬ФЩёщҫЭ№ЕөдёЕВКЗуҪвЛщійИЎөД3ИЛІ»КфУЪН¬Т»ЧйөДёЕВКЈ»
ЈЁ2Ј©ПИЗу![]() өДЛщУРИЎЦөЈ¬ФЩЗуҪв·ЦІјБРәНКэС§ЖЪНы.
өДЛщУРИЎЦөЈ¬ФЩЗуҪв·ЦІјБРәНКэС§ЖЪНы.
ИПОӘЎ°іЙјЁУЕРгЎұөДұ»ІвСйС§Йъ№ІУРБҪЧйЈ¬ЖдЖөВК·ЦІјОӘ0.24Ј¬0.16Ј¬ёщҫЭ·ЦІгійСщөД·Ҫ·ЁҝЙЦӘЈ¬БҪЧйійИЎөДИЛКэ·ЦұрОӘ6ИЛЈ¬4ИЛ.
ЈЁ1Ј©ҙУ10ИЛЦРИОСЎ3ИЛЈ¬УР![]() ЦЦІ»Н¬ЗйҝцЈ¬ійИЎөД3ИЛІ»КфУЪН¬Т»ЧйөДЗйҝцУР
ЦЦІ»Н¬ЗйҝцЈ¬ійИЎөД3ИЛІ»КфУЪН¬Т»ЧйөДЗйҝцУР![]() Ј¬
Ј¬
№КЛщійИЎөД3ИЛІ»КфУЪН¬Т»ЧйөДёЕВКОӘ![]() Ј»
Ј»
ЈЁ2Ј©УЙМхјюҝЙөГ![]() өДИЎЦөҝЙДЬУР0Ј¬1Ј¬2Ј¬3Ј¬ЗТ
өДИЎЦөҝЙДЬУР0Ј¬1Ј¬2Ј¬3Ј¬ЗТ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.
![]() өД·ЦІјБРОӘ
өД·ЦІјБРОӘ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() өДКэС§ЖЪНыОӘ
өДКэС§ЖЪНыОӘ![]() .
.


 КАјН°ЩНЁЦчМеҝОМГРЎС§ҝОКұН¬ІҪҙпұкПөБРҙр°ё
КАјН°ЩНЁЦчМеҝОМГРЎС§ҝОКұН¬ІҪҙпұкПөБРҙр°ё КАјН°ЩНЁУЕБ·ІвПөБРҙр°ё
КАјН°ЩНЁУЕБ·ІвПөБРҙр°ё °Щ·ЦС§ЙъЧчТөұҫМвБ·НхПөБРҙр°ё
°Щ·ЦС§ЙъЧчТөұҫМвБ·НхПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЛДАвЧ¶P©ҒABCDөДөЧГжABCDОӘЦұҪЗМЭРОЈ¬AD//BCЈ¬ЗТ![]() Ј¬BCЎНDCЈ¬ЎПBAD=60ЎгЈ¬ЖҪГжPADЎНөЧГжABCDЈ¬EОӘADөДЦРөгЈ¬ЎчPADОӘөИұЯИэҪЗРОЈ¬MКЗАвPCЙПөДТ»өгЈ¬Йи
Ј¬BCЎНDCЈ¬ЎПBAD=60ЎгЈ¬ЖҪГжPADЎНөЧГжABCDЈ¬EОӘADөДЦРөгЈ¬ЎчPADОӘөИұЯИэҪЗРОЈ¬MКЗАвPCЙПөДТ»өгЈ¬Йи![]() ЈЁMУлCІ»ЦШәПЈ©Ј®
ЈЁMУлCІ»ЦШәПЈ©Ј®
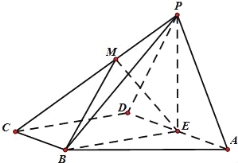
ЈЁ1Ј©ЗуЦӨЈәCDЎНDPЈ»
ЈЁ2Ј©ИфPAЎОЖҪГжBMEЈ¬ЗуkөДЦөЈ»
ЈЁ3Ј©Иф¶юГжҪЗM©ҒBE©ҒAөДЖҪГжҪЗОӘ150ЎгЈ¬ЗуkөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіөҘО»№ІУР10ГыФұ№ӨЈ¬ЛыГЗДіДкөДКХИлИзПВұнЈә
Фұ№ӨұаәЕ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ДкРҪЈЁНтФӘЈ© | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
ЈЁ1Ј©ЗуёГөҘО»Фұ№ӨөұДкДкРҪөДЖҪҫщЦөәНЦРО»КэЈ»
ЈЁ2Ј©ТСЦӘФұ№ӨДкРҪКХИлУл№ӨЧчДкПЮіЙХэПа№Ш№ШПөЈ¬ДіФұ№Ө№ӨЧчөЪТ»ДкЦБөЪЛДДкөДДкРҪ·ЦұрОӘ4НтФӘЎў5.5НтФӘЎў6НтФӘЎў8.5НтФӘЈ¬ФӨІвёГФұ№ӨөЪБщДкөДДкРҪОӘ¶аЙЩЈҝ
ёҪЈәПЯРФ»Ш№й·ҪіМ![]() ЦРПөКэјЖЛ㹫КҪ·ЦұрОӘЈә
ЦРПөКэјЖЛ㹫КҪ·ЦұрОӘЈә Ј¬
Ј¬![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() Ўў
Ўў![]() ОӘСщұҫҫщЦө.
ОӘСщұҫҫщЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ТСЦӘНЦФІCЈә![]() (aЈҫbЈҫ0)№эөг
(aЈҫbЈҫ0)№эөг![]() Ј¬АлРДВКОӘ
Ј¬АлРДВКОӘ![]() .
.
ЈЁ1Ј©ЗуНЦФІCөД·ҪіМЈ»
ЈЁ2Ј©ИфРұВКОӘ![]() өДЦұПЯlУлНЦФІCҪ»УЪAЈ¬BБҪөгЈ¬КФМҪҫҝ
өДЦұПЯlУлНЦФІCҪ»УЪAЈ¬BБҪөгЈ¬КФМҪҫҝ![]() КЗ·сОӘ¶ЁЦөЈҝИфКЗ¶ЁЦөЈ¬ФтЗуіцҙЛ¶ЁЦөЈ»ИфІ»КЗ¶ЁЦөЈ¬ЗлЛөГчАнУЙЈ®
КЗ·сОӘ¶ЁЦөЈҝИфКЗ¶ЁЦөЈ¬ФтЗуіцҙЛ¶ЁЦөЈ»ИфІ»КЗ¶ЁЦөЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ҫШРО![]() ЛщФЪЖҪГжУл°лФІ»Ў
ЛщФЪЖҪГжУл°лФІ»Ў![]() ЛщФЪЖҪГжҙ№ЦұЈ¬
ЛщФЪЖҪГжҙ№ЦұЈ¬![]() КЗ
КЗ![]() ЙПТмУЪ
ЙПТмУЪ![]() Ј¬
Ј¬![]() өДөгЈ®
өДөгЈ®
ЈЁ1Ј©ЦӨГчЈәЖҪГж![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁ2Ј©ФЪПЯ¶О![]() ЙПКЗ·сҙжФЪөг
ЙПКЗ·сҙжФЪөг![]() Ј¬К№өГ
Ј¬К№өГ![]() ЖҪГж
ЖҪГж![]() ЈҝЛөГчАнУЙЈ®
ЈҝЛөГчАнУЙЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝГьМв![]() ·ҪіМ
·ҪіМ![]() ұнКҫЛ«ЗъПЯЈ»ГьМв
ұнКҫЛ«ЗъПЯЈ»ГьМв![]() І»өИКҪ
І»өИКҪ![]() өДҪвјҜКЗ
өДҪвјҜКЗ![]() .
. ![]() ОӘјЩЈ¬
ОӘјЩЈ¬ ![]() ОӘХжЈ¬Зу
ОӘХжЈ¬Зу![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ўҫҙр°ёЎҝ![]()
ЎҫҪвОцЎҝКФМв·ЦОцЈәУЙГьМв![]() ·ҪіМ
·ҪіМ![]() ұнКҫЛ«ЗъПЯЈ¬Зуіц
ұнКҫЛ«ЗъПЯЈ¬Зуіц![]() өДИЎЦө·¶О§Ј¬УЙГьМв
өДИЎЦө·¶О§Ј¬УЙГьМв![]() І»өИКҪ
І»өИКҪ![]() өДҪвјҜКЗ
өДҪвјҜКЗ![]() Ј¬Зуіц
Ј¬Зуіц![]() өДИЎЦө·¶О§Ј¬УЙ
өДИЎЦө·¶О§Ј¬УЙ![]() ОӘјЩЈ¬
ОӘјЩЈ¬ ![]() ОӘХжЈ¬өГіц
ОӘХжЈ¬өГіц![]() Т»ХжТ»јЩЈ¬·ЦБҪЦЦЗйҝцјҙҝЙөГіц
Т»ХжТ»јЩЈ¬·ЦБҪЦЦЗйҝцјҙҝЙөГіц![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
КФМвҪвОцЈә
![]() Хж
Хж ![]()
![]() Ј¬
Ј¬
![]() Хж
Хж ![]() »т
»т![]()
![]()
Ўа![]()
![]() Хж
Хж![]() јЩ
јЩ ![]()
![]() јЩ
јЩ![]() Хж
Хж ![]()
Ўа![]() ·¶О§ОӘ
·¶О§ОӘ![]()
ЎҫМвРНЎҝҪвҙрМв
ЎҫҪбКшЎҝ
18
ЎҫМвДҝЎҝИзНјЈ¬Йи![]() КЗФІ
КЗФІ![]() ЙПөД¶ҜөгЈ¬өг
ЙПөД¶ҜөгЈ¬өг![]() КЗ
КЗ![]() ФЪ
ФЪ![]() ЦбЙПөДН¶У°Ј¬
ЦбЙПөДН¶У°Ј¬ ![]() ОӘ
ОӘ![]() ЙПТ»өгЈ¬ЗТ
ЙПТ»өгЈ¬ЗТ![]() .
.

ЈЁ1Ј©өұ![]() ФЪФІЙПФЛ¶ҜКұЈ¬Зуөг
ФЪФІЙПФЛ¶ҜКұЈ¬Зуөг![]() өД№мјЈ
өД№мјЈ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©Зу№эөг![]() ЗТРұВКОӘ
ЗТРұВКОӘ![]() өДЦұПЯұ»
өДЦұПЯұ»![]() ЛщҪШПЯ¶ОөДіӨ¶И.
ЛщҪШПЯ¶ОөДіӨ¶И.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЦұПЯlөДІОКэ·ҪіМОӘ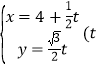 ОӘІОКэ
ОӘІОКэ![]() Ј¬ТФЧшұкФӯөгОӘј«өгЈ¬xЦбөДХэ°лЦбОӘј«ЦбҪЁҪЁБўј«ЧшұкПөЈ¬ЗъПЯCөДј«Чшұк·ҪіМОӘ
Ј¬ТФЧшұкФӯөгОӘј«өгЈ¬xЦбөДХэ°лЦбОӘј«ЦбҪЁҪЁБўј«ЧшұкПөЈ¬ЗъПЯCөДј«Чшұк·ҪіМОӘ![]() Ј®
Ј®
![]() ЗуЗъПЯCөДЦұҪЗЧшұк·ҪіМУлЦұПЯlөДј«Чшұк·ҪіМЈ»
ЗуЗъПЯCөДЦұҪЗЧшұк·ҪіМУлЦұПЯlөДј«Чшұк·ҪіМЈ»
![]() ўт
ўт![]() ИфЦұПЯ
ИфЦұПЯ![]() УлЗъПЯCҪ»УЪөг
УлЗъПЯCҪ»УЪөг![]() І»Н¬УЪФӯөг
І»Н¬УЪФӯөг![]() Ј¬УлЦұПЯlҪ»УЪөгBЈ¬Зу
Ј¬УлЦұПЯlҪ»УЪөгBЈ¬Зу![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПИФД¶БПВБРІ»өИКҪөДЦӨ·ЁЈ¬ФЩҪвҫцәуГжөДОКМвЈә
ТСЦӘ![]() Ј¬
Ј¬![]() Ј¬ЗуЦӨЈә
Ј¬ЗуЦӨЈә![]() .
.
ЦӨГчЈә№№ФмәҜКэ![]() Ј¬
Ј¬
јҙ![]()
![]() .
.
ТтОӘ¶ФТ»ЗР![]() Ј¬әгУР
Ј¬әгУР![]() Ј¬
Ј¬
ЛщТФ![]() Ј¬ҙУ¶шөГ
Ј¬ҙУ¶шөГ![]() .
.
ЈЁ1Ј©Иф![]() Ј¬
Ј¬![]() Ј¬ЗлРҙіцЙПКцҪбВЫөДНЖ№гКҪЈ»
Ј¬ЗлРҙіцЙПКцҪбВЫөДНЖ№гКҪЈ»
ЈЁ2Ј©ІОҝјЙПКцЦӨ·ЁЈ¬¶ФДгНЖ№гөДҪбВЫјУТФЦӨГч.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪ·ўЙъДі№«№ІОАЙъКВјюЖЪјдЈ¬УРЧЁТө»ъ№№ИПОӘёГКВјюФЪТ»¶ОКұјдГ»УР·ўЙъФЪ№жДЈИәМеёРИҫөДұкЦҫОӘЎ°Б¬Рш10МмЈ¬ГҝМмРВФцТЙЛЖІЎАэІ»і¬№э7ИЛЎұ.ёщҫЭ№эИҘ10МмјЧЎўТТЎўұыЎў¶ЎЛДөШРВФцТЙЛЖІЎАэКэҫЭЈ¬Т»¶Ё·ыәПёГұкЦҫөДКЗ
A. јЧөШЈәЧЬМеҫщЦөОӘ3Ј¬ЦРО»КэОӘ4 B. ТТөШЈәЧЬМеҫщЦөОӘ1Ј¬ЧЬМе·ҪІоҙуУЪ0
C. ұыөШЈәЦРО»КэОӘ2Ј¬ЦЪКэОӘ3 D. ¶ЎөШЈәЧЬМеҫщЦөОӘ2Ј¬ЧЬМе·ҪІоОӘ3
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com