
°Њћвƒњ°њ“ї÷ї“©”√ј•≥жµƒ≤ъ¬— эy”л“їґ®ЈґќІƒЏµƒќ¬ґ»x”–єЎ£ђѕ÷ ’ЉѓЅЋЄ√÷÷“©”√ј•≥жµƒ6„йєџ≤в эЊЁ»зѕ¬±н£Ї
ќ¬ґ»x/°ж | 21 | 23 | 24 | 27 | 29 | 32 |
≤ъ¬— эy/Єц | 6 | 11 | 20 | 27 | 57 | 77 |
Њ≠Љ∆Ћгµ√£Ї
![]() £ђ
£ђ![]() £ђ
£ђ![]() ѕя–‘їЎєйƒ£–Ќµƒ≤–≤о∆љЈљЇЌ
ѕя–‘їЎєйƒ£–Ќµƒ≤–≤о∆љЈљЇЌ![]() £ђ
£ђ![]() £ђ
£ђ
∆д÷–![]() Ј÷±рќ™єџ≤в эЊЁ÷–µƒќ¬ґ»ЇЌ≤ъ¬— э£ђ
Ј÷±рќ™єџ≤в эЊЁ÷–µƒќ¬ґ»ЇЌ≤ъ¬— э£ђ![]()
£®1£©»ф”√ѕя–‘їЎєйƒ£–Ќ£ђ«уyєЎ”ЏxµƒїЎєйЈљ≥ћ![]() £®ЊЂ»Јµљ0.1£©£ї
£®ЊЂ»Јµљ0.1£©£ї
£®2£©»ф”√Ј«ѕя–‘їЎєйƒ£–Ќ«уµ√yєЎ”ЏxµƒїЎєйЈљ≥ћќ™![]() £ђ«“ѕаєЎ÷Є э
£ђ«“ѕаєЎ÷Є э![]() .
.
Ґў ‘”л1÷–µƒїЎєйƒ£–Ќѕа±»£ђ”√![]() Ћµ√чƒƒ÷÷ƒ£–ЌµƒƒвЇѕ–ІєыЄьЇ√.
Ћµ√чƒƒ÷÷ƒ£–ЌµƒƒвЇѕ–ІєыЄьЇ√.
ҐЏ”√ƒвЇѕ–ІєыЇ√µƒƒ£–Ќ‘§≤вќ¬ґ»ќ™35°ж ±Є√”√ƒƒ÷÷“©”√ј•≥жµƒ≤ъ¬— э£®љбєы»°’ы э£©
Єљ£Ї“ї„й эЊЁ![]() ∆дїЎєй÷±ѕя
∆дїЎєй÷±ѕя![]() µƒ–±¬ ЇЌљЎЊаµƒ„о–°ґю≥ЋєјЉ∆ќ™
µƒ–±¬ ЇЌљЎЊаµƒ„о–°ґю≥ЋєјЉ∆ќ™ £ђ
£ђ![]() £їѕаєЎ÷Є э
£їѕаєЎ÷Є э .
.
°Њір∞Є°њ£®1£©![]() £®2£©Ґў”√Ј«ѕя–‘їЎєйƒ£–ЌƒвЇѕ–ІєыЄьЇ√£їҐЏ190Єц
£®2£©Ґў”√Ј«ѕя–‘їЎєйƒ£–ЌƒвЇѕ–ІєыЄьЇ√£їҐЏ190Єц
°Њљвќц°њ
£®1£©«у≥ц![]() °Ґ
°Ґ![]() Їуіъ»лєЂ љ÷±љ”Љ∆Ћгµ√
Їуіъ»лєЂ љ÷±љ”Љ∆Ћгµ√![]() °Ґ
°Ґ![]() £ђЉіњ…µ√љв£ї
£ђЉіњ…µ√љв£ї
£®2£©«у≥цѕя–‘їЎєйƒ£–ЌµƒѕаєЎ÷Є э£ђ”л![]() ±»љѕЉіњ…µ√љв£ї
±»љѕЉіњ…µ√љв£ї
£®3£©÷±љ”∞—![]() іъ»л
іъ»л![]() £ђЉ∆ЋгЉіњ…µ√љв.
£ђЉ∆ЋгЉіњ…µ√љв.
£®1£©”…ћв“в![]() £ђ‘т
£ђ‘т![]() £ђ
£ђ![]() £ђ
£ђ
 £ђ
£ђ![]() £ђ
£ђ
yєЎ”Џxµƒѕя–‘їЎєйЈљ≥ћќ™![]() .
.
£®2£©Ґўґ‘”Џѕя–‘їЎєйƒ£–Ќ£ђ![]() £ђ
£ђ![]() £ђ
£ђ
ѕаєЎ÷Є эќ™
![]()
![]()
“тќ™![]() £ђЋщ“‘”√Ј«ѕя–‘їЎєйƒ£–ЌƒвЇѕ–ІєыЄьЇ√.
£ђЋщ“‘”√Ј«ѕя–‘їЎєйƒ£–ЌƒвЇѕ–ІєыЄьЇ√.
ҐЏµ±![]() £ђ ±
£ђ ±![]()
![]()
![]() £®Єц£©
£®Єц£©
Ћщ“‘ќ¬ґ»ќ™![]() ±£ђЄ√÷÷“©”√ј•≥жµƒ≤ъ¬— эєјЉ∆ќ™190Єц.
±£ђЄ√÷÷“©”√ј•≥жµƒ≤ъ¬— эєјЉ∆ќ™190Єц.


 ÷–њЉљвґЅњЉµгЊЂЅЈѕµЅ–ір∞Є
÷–њЉљвґЅњЉµгЊЂЅЈѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™µ»±» эЅ–{an}µƒЄчѕоЊщќ™’э э£ђ2a2©Б5a1=3£ђa3a7=9a42£ї
£®1£©«у эЅ–{an}µƒЌ®ѕоєЂ љ£ї
£®2£©…иbn=anlog3an£ђ«у эЅ–{bn}µƒ«∞nѕоЇЌSn£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Їѓ э![]() .
.
£®1£©»ф![]() ‘Џґ®“е”т…ѕ≤їµ•µч£ђ«у
‘Џґ®“е”т…ѕ≤їµ•µч£ђ«у![]() µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї
£®2£©…и![]() Ј÷±р «
Ј÷±р «![]() µƒЉЂіу÷µЇЌЉЂ–°÷µ£ђ«“
µƒЉЂіу÷µЇЌЉЂ–°÷µ£ђ«“![]() £ђ«у
£ђ«у![]() µƒ»°÷µЈґќІ.
µƒ»°÷µЈґќІ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Їѓ э![]() ,
,![]() «“
«“![]() .
.
£®1£©»фЇѓ э![]() ‘Џ
‘Џ![]() …ѕЇг”–“в“е£ђ«у
…ѕЇг”–“в“е£ђ«у![]() µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї
£®2£© «Јсіж‘Џ µ э![]() £ђ єЇѓ э
£ђ єЇѓ э![]() ‘Џ«шЉд
‘Џ«шЉд![]() …ѕќ™‘цЇѓ э£ђ«“„оіу÷µќ™
…ѕќ™‘цЇѓ э£ђ«“„оіу÷µќ™![]() £њ»фіж‘Џ«у≥ц
£њ»фіж‘Џ«у≥ц![]() µƒ÷µ£ђ»ф≤їіж‘Џ«лЋµ√чјн”….
µƒ÷µ£ђ»ф≤їіж‘Џ«лЋµ√чјн”….
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њѕ¬ЌЉќ™ƒ≥≤÷њв“ї≤а«љ√жµƒ Њ“вЌЉ£ђ∆дѕ¬≤њ «ЊЎ–ќABCD£ђ…ѕ≤њ «‘≤ї°AB£ђЄ√‘≤ї°Ћщ‘Џµƒ‘≤–ƒќ™O£ђќ™ЅЋµчљЏ≤÷њвƒЏµƒ ™ґ»ЇЌќ¬ґ»£ђѕ÷“™‘Џ«љ√ж…ѕњ™“їЄцЊЎ–ќµƒЌ®Јзі∞EFGH£®∆д÷–E£ђF‘Џ‘≤ї°AB…ѕ£ђG£ђH‘Џѕ“AB…ѕ£©.єэO„ч![]() £ђљїAB ”ЏM£ђљїEF”ЏN£ђљї‘≤ї°AB”ЏP£ђ“—÷™
£ђљїAB ”ЏM£ђљїEF”ЏN£ђљї‘≤ї°AB”ЏP£ђ“—÷™![]() £®µ•ќї£Їm£©£ђЉ«Ќ®Јзі∞EFGHµƒ√жїэќ™S£®µ•ќї£Ї
£®µ•ќї£Їm£©£ђЉ«Ќ®Јзі∞EFGHµƒ√жїэќ™S£®µ•ќї£Ї![]() £©
£©
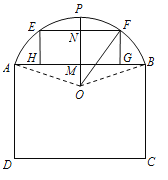
£®1£©∞іѕ¬Ѕ–“™«уљ®ЅҐЇѓ эєЎѕµ љ£Ї
£®i£©…и![]() £ђљЂS±н Њ≥…
£ђљЂS±н Њ≥…![]() µƒЇѓ э£ї
µƒЇѓ э£ї
£®ii£©…и![]() £ђљЂS±н Њ≥…
£ђљЂS±н Њ≥…![]() µƒЇѓ э£ї
µƒЇѓ э£ї
£®2£© ‘ќ Ќ®Јзі∞µƒЄяґ»MNќ™ґа…ў ±£ђЌ®Јзі∞EFGHµƒ√жїэS„оіу£њ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Їѓ э![]() ,
,![]() «“
«“![]() .
.
£®1£©»фЇѓ э![]() ‘Џ
‘Џ![]() …ѕЇг”–“в“е£ђ«у
…ѕЇг”–“в“е£ђ«у![]() µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї
£®2£© «Јсіж‘Џ µ э![]() £ђ єЇѓ э
£ђ єЇѓ э![]() ‘Џ«шЉд
‘Џ«шЉд![]() …ѕќ™‘цЇѓ э£ђ«“„оіу÷µќ™
…ѕќ™‘цЇѓ э£ђ«“„оіу÷µќ™![]() £њ»фіж‘Џ«у≥ц
£њ»фіж‘Џ«у≥ц![]() µƒ÷µ£ђ»ф≤їіж‘Џ«лЋµ√чјн”….
µƒ÷µ£ђ»ф≤їіж‘Џ«лЋµ√чјн”….
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉЋщ Њ£ђ‘Џ’эЈљћеABCDA1B1C1D1÷–£ђ…иѕяґќA1C”л∆љ√жABC1D1љї”ЏµгQ£ђ«у÷§£ЇB£ђQ£ђD1»эµгє≤ѕя£Ѓ
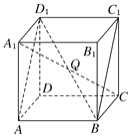
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉЋщ Њµƒ°∞8°±„÷–ќ«ъѕя «”…ЅљЄцєЎ”Џx÷бґ‘≥∆µƒ∞л‘≤ЇЌ“їЄцЋЂ«ъѕяµƒ“ї≤њЈ÷„й≥…µƒЌЉ–ќ£ђ∆д÷–…ѕ∞лЄц‘≤Ћщ‘Џ‘≤Јљ≥ћ «x2+y2©Б4y©Б4£љ0£ђЋЂ«ъѕяµƒ„у°Ґ”“ґ•µгA°ҐB «Є√‘≤”лx÷бµƒљїµг£ђЋЂ«ъѕя”л∞л‘≤ѕаљї”Џ”лx÷б∆љ––µƒ÷±ЊґµƒЅљґЋµг£Ѓ
£®1£© ‘«уЋЂ«ъѕяµƒ±к„ЉЈљ≥ћ£ї
£®2£©Љ«ЋЂ«ъѕяµƒ„у°Ґ”“љєµгќ™F1°ҐF2£ђ ‘‘Џ°∞8°±„÷–ќ«ъѕя…ѕ«уµгP£ђ єµ√°ѕF1PF2 «÷±љ«£Ѓ
£®3£©єэµгA„ч÷±ѕяlЈ÷±рљї°∞8°±„÷–ќ«ъѕя÷–…ѕ°Ґѕ¬ЅљЄц∞л‘≤”ЏµгM°ҐN£ђ«у|MN|µƒ„оіу≥§ґ»£Ѓ
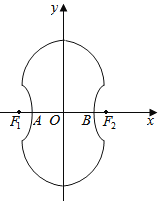
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ’эЈљћеABCD©БA1B1C1D1÷–£ђAM°Ќ∆љ√жA1BD£ђіє„гќ™M£ђ“‘ѕ¬ЋƒЄцљб¬џ÷–’э»ЈµƒЄц эќ™£®°°°°£©
ҐўAMіє÷±”Џ∆љ√жCB1D1£ї
ҐЏ÷±ѕяAM”лBB1Ћщ≥…µƒљ«ќ™45°г£ї
ҐџAMµƒ—”≥§ѕяєэµгC1£ї
Ґ№÷±ѕяAM”л∆љ√жA1B1C1D1Ћщ≥…µƒљ«ќ™60°г
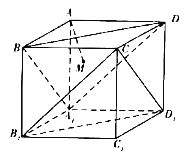
A. 1 B. 2 C. 3 D. 4
≤йњіір∞ЄЇЌљвќц>>
∞ўґ»÷¬–≈ - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com