
| |||||||||||||||
(1) |
解:∵点A1(x1,y1)在抛物线y=x2上,且x1=1,∴y1=1,即A点坐标是(1,1). 又∵l1的斜率为 ∴l1的方程为2x-y-1=0. 分析:利用导数的几何意义求出切线ln的斜率关于切点坐标的表达式 |
(2) |
∵An在抛物线上,∴yn= ∵ln的斜率为 ∴ ∴ 分析:由斜率公式得数列{xn}的递推关系. |
(3) |
∵bn=n· ①-②,得 ∴Sn=4 ∵当>3时, 又数列 点评:当点的坐标所成的数列的通项与曲线的切线相关时,可利用导数的几何意义求出相关点的坐标关于切点坐标的关系式,设法得到数列的通项. |


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
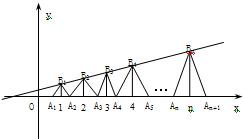 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数y=
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数y=| 1 |
| 4 |
| 1 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数y=
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数y=| 1 |
| 4 |
| 1 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| x |
| 1 |
| n |
. |
| y |
| 1 |
| n |
. |
| x |
. |
| y |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com