Question

【题目】在对人们的休闲方式的一次调查中，用简单随机抽样方法调查了125人，其中女性70人，男性55人.女性中有40人主要的休闲方式是看电视，另外30人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外35人主要的休闲方式是运动.

（1）根据以上数据建立一个列联表；

（2）能否在犯错误的概率不超过0.025的前提下，认为性别与休闲方式有关系?

（3）在休闲方式为看电视的人中按分层抽样方法抽取6人参加某机构组织的健康讲座，讲座结束后再从这6人中抽取2人作反馈交流，求参加交流的恰好为2位女性的概率.

附：

P（ ）	0.05	0.025	0.010
k	3.841	5.024	6.635

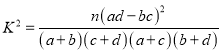
休闲方式 性别	看电视	运动	合计
女
男
合计

Answer 1

【答案】(1)答案见解析；(2)在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”.(3)0.4.

【解析】【试题分析】（1）根据题目所给已知条件填写好联表；（2）通过计算，所以在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”. （3）按分层抽样，则男性有人，女性有人，通过列举法可求得基本事件总数有种，符合要求的有种，故概率为.

【试题解析】

(1) 列联表为：

休闲方式 性别	看电视	运动	合计
女	40	30	70
男	20	35	55
合计	60	65	125

（2）假设“休闲方式与性别无关”，计算

．

因为，所以在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”.

（3）休闲方式为看电视的共60人，按分层抽样方法抽取6人，则男性有2人，可记为A、B，女性4人，可记为c，d，e、f.

现从6人中抽取2人，基本事件是AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf、cd、ce、cf、de、df、ef共15种不同的方法，恰是2女性的有cd、ce、cf、de、df、ef共6种不同的方法，故所求概率为．