
【题目】已知袋子中放有大小和形状相同标号分别是0,1,2的小球若干,其中标号为0的小球1个,标号为1的小球2个,标号为2的小球n个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求n的值
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的球标号为b.
①记“![]() ”为事件A,求事件A的概率;
”为事件A,求事件A的概率;
②在区间![]() 内任取2个实数x,y,求事件“
内任取2个实数x,y,求事件“![]() 恒成立”的概率.
恒成立”的概率.
【答案】(1) ![]() ;(2) ①
;(2) ①![]() ;②
;②![]()
【解析】
(1)由古典概型公式列出方程求解即可;(2) ①从袋子中不放回的随机取2个球共有12个基本事件,确定![]() 的事件个数代入古典概型概率计算公式即可得解;②事件B等价于
的事件个数代入古典概型概率计算公式即可得解;②事件B等价于![]() 恒成立,
恒成立,![]() 可以看做平面中的点,确定全部结果所构成的区域,事件B构成的区域,利用几何概型面积型计算公式即可得解.
可以看做平面中的点,确定全部结果所构成的区域,事件B构成的区域,利用几何概型面积型计算公式即可得解.
(1)依题意![]() ;
;
(2)将标号为0的小球记为0,标号为1的小球记为A,B,标号为2的小球记为2,则从袋子中两次不放回地随机抽取2个小球可能的结果为:![]()
![]() 共12种,
共12种,
①事件A包含4种:![]() ,所以
,所以![]() ;
;
②因为![]() 的最大值为4,所以事件B等价于
的最大值为4,所以事件B等价于![]() 恒成立,
恒成立,
![]() 可以看做平面中的点,则全部结果所构成的区域
可以看做平面中的点,则全部结果所构成的区域![]() ,
,
事件B所构成的区域![]() ,
,
则![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示. 已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .

(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中抽取教职工多少名?
(3)已知![]() ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.
的中点.![]() 为面对角线
为面对角线![]() 上任一点,则下列说法正确的是( )
上任一点,则下列说法正确的是( )

A.平面![]() 内存在直线与
内存在直线与![]() 平行
平行
B.平面![]() 截正方体
截正方体![]() 所得截面面积为
所得截面面积为![]()
C.直线![]() 和
和![]() 所成角可能为60°
所成角可能为60°
D.直线![]() 和
和![]() 所成角可能为30°
所成角可能为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知圆方程为![]() ,过圆上任意一点作圆的切线,切线与椭圆
,过圆上任意一点作圆的切线,切线与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,设
为坐标原点,设![]() 为
为![]() 的中点,求
的中点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 是由两个定点
是由两个定点![]() 和点
和点![]() 的距离之积等于
的距离之积等于![]() 的所有点组成的,对于曲线
的所有点组成的,对于曲线![]() ,有下列四个结论:①曲线
,有下列四个结论:①曲线![]() 是轴对称图形;②曲线
是轴对称图形;②曲线![]() 上所有的点都在单位圆
上所有的点都在单位圆![]() 内;③曲线
内;③曲线![]() 是中心对称图形;④曲线
是中心对称图形;④曲线![]() 上所有点的纵坐标
上所有点的纵坐标![]() .其中,所有正确结论的序号是______.
.其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
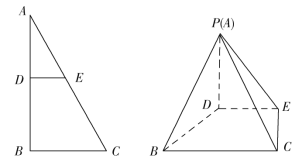
如图,已知![]() 是以
是以![]() 的直角三角形铁皮,
的直角三角形铁皮,![]() 米,
米,![]() 分别是边
分别是边![]() 上不与端点重合的动点,且
上不与端点重合的动点,且![]() .现将
.现将![]() 铁皮沿
铁皮沿![]() 折起至
折起至![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,连接
,连接![]() ,如图所示.现要制作一个四棱锥
,如图所示.现要制作一个四棱锥![]() 的封闭容器,其中
的封闭容器,其中![]() 铁皮和直角梯形
铁皮和直角梯形![]() 铁皮分别是这个封闭容器的一个侧面和底面,其他三个侧面用相同材料的铁皮无缝焊接密封而成(假设制作过程中不浪费材料,且铁皮厚度忽略不计).
铁皮分别是这个封闭容器的一个侧面和底面,其他三个侧面用相同材料的铁皮无缝焊接密封而成(假设制作过程中不浪费材料,且铁皮厚度忽略不计).
(1)若![]() 为
为![]() 边的中点,求制作三个新增侧面的铁皮面积是多少平方米?
边的中点,求制作三个新增侧面的铁皮面积是多少平方米?
(2)求这个封闭容器的最大体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() 为等比数列,求出
为等比数列,求出![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() 的前n项和
的前n项和![]() ,并判断是否存在正整数n使得
,并判断是否存在正整数n使得![]() 成立?若存在求出所有n值;若不存在说明理由.
成立?若存在求出所有n值;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图.
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com