
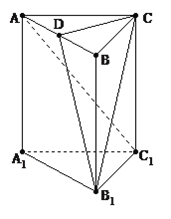
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC, 点D是AB的中点.
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求证:AC1∥平面CDB1;
(Ⅲ)线段AB上是否存在点M,使得A1M⊥平面CDB1?
【答案】(1)见解析;(2)见解析.(3)见解析
【解析】试题分析:(Ⅰ)由已知先证明CD⊥AB,又在直三棱柱ABC-A1B1C1中,AA1⊥CD,且AB∩AA1=A,即可证明CD⊥平面A1ABB1;
(Ⅱ)连结BC1,设BC1与B1C的交点为E,连接DE,证得DE∥AC1;由线面平行的判定定理即可证明AC1∥平面CDB1;
(Ⅲ)存在点M为B,由(Ⅰ)知CD⊥平面A1ABB1,又A1BA1ABB1,可得CD⊥A1B,由已知可得A1A:AB=BD:BB1=1: ![]() ,即证明A1B⊥B1D,又CD∩B1D=D,从而证明A1B⊥平面CDB1.
,即证明A1B⊥B1D,又CD∩B1D=D,从而证明A1B⊥平面CDB1.
试题解析:
证明:(Ⅰ)∵ABC-A1B1C1是直三棱柱,∴平面ABC⊥平面A1ABB1, ∵AC=BC,点D是AB的中点,∴CD⊥AB, 面ABC![]() 面A1ABB1 =AB ∴CD⊥平面A1ABB1
面A1ABB1 =AB ∴CD⊥平面A1ABB1
(Ⅱ)连结BC1,设BC1与B1C的交点为E,连结DE.∵D是AB的中点,E是BC1的中点,∴DE∥AC1
∵DE![]() 平面CDB1 , AC1
平面CDB1 , AC1![]() 平面CDB1, ∴AC1∥平面CDB1.
平面CDB1, ∴AC1∥平面CDB1.
(Ⅲ)存在点M为B. 由(Ⅰ)知 CD⊥平面A1ABB,又 A1B![]() 平面A1ABB,∴CD⊥A1B
平面A1ABB,∴CD⊥A1B
∵AC=BC=CC1,AC⊥BC,点D是AB的中点.
∴A1A : AB=BD : BB1=1: ![]() , ∴A1B⊥B1D, 又CD
, ∴A1B⊥B1D, 又CD![]() B1D=D, ∴A1B⊥平面CDB1.
B1D=D, ∴A1B⊥平面CDB1.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
(1)设bn=an+1+an(n∈N+),求证{bn}是等比数列;
(2)(i)求数列{an}的通项公式;
(ii)求证:对于任意n∈N+都有 ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() <
< ![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB平面PAD,△PAD是正三角形,DC//AB,DA=DC=2AB.
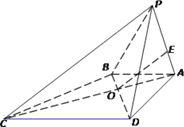
(1)若点E为棱PA上一点,且OE∥平面PBC,求![]() 的值;
的值;
(2)求证:平面PBC平面PDC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列{an}前n项和为Sn , 且 ![]() (n∈N+)
(n∈N+)
(1)求数列{an}的通项公式;
(2)若 ![]() ,数列{bn}的前n项和为Tn , 证明:T2n﹣1>1>T2n(n∈N+).
,数列{bn}的前n项和为Tn , 证明:T2n﹣1>1>T2n(n∈N+).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() +
+![]() =1的左、右焦点分别为F1,F2,一条直线
=1的左、右焦点分别为F1,F2,一条直线![]() 经过点F1与椭圆交于A,B两点.
经过点F1与椭圆交于A,B两点.
(1)求△ABF2的周长;
(2)若![]() 的倾斜角为
的倾斜角为![]() ,求弦长|AB|.
,求弦长|AB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com