
【题目】若存在正数x,y,使得![]() ,其中e为自然对数的底数,则实数
,其中e为自然对数的底数,则实数![]() 的取值范围是_____________.
的取值范围是_____________.
【答案】(![]() ,0)
,0)![]() [
[![]() ,
,![]() )
)
【解析】
根据函数与方程的关系将方程进行转化,利用换元法转化为方程有解,构造函数求函数的导数,利用函数极值和单调性的关系进行求解即可.
由![]() 得x+s(y﹣2ex)ln
得x+s(y﹣2ex)ln![]() =0,
=0,
即1+s(![]() ﹣2e)ln
﹣2e)ln![]() =0,
=0,
即设t=![]() ,则t>0,
,则t>0,
则条件等价为1+s(t﹣2e)lnt=0,
即(t﹣2e)lnt=![]() 有解,
有解,
设g(t)=(t﹣2e)lnt,
g′(t)=lnt+1﹣![]() 为增函数,
为增函数,
∵g′(e)=lne+1﹣![]() =1+1﹣2=0,
=1+1﹣2=0,
∴当t>e时,g′(t)>0,
当0<t<e时,g′(t)<0,
即当t=e时,函数g(t)取得极小值,为g(e)=(e﹣2e)lne=﹣e,
即g(t)≥g(e)=﹣e,
若(t﹣2e)lnt=![]() 有解,
有解,
则![]() ≥﹣e,即
≥﹣e,即![]() ≤e,
≤e,
则s<0或s≥![]() ,
,
故答案为:s<0或s≥![]() .
.


科目:高中数学 来源: 题型:
【题目】某单位开展岗前培训期间,甲、乙2人参加了5次考试,成绩统计如下:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩 | 82 | 82 | 79 | 95 | 87 |
乙的成绩 | 95 | 75 | 80 | 90 | 85 |
(1)根据有关统计知识回答问题:若从甲、乙2人中选出1人上岗,你认为选谁合适?请说明理由;
(2)根据有关概率知识解答以下问题:若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”.由上述5次成绩统计,任意抽查两次考试,求至少有一次考试两人“水平相当”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某二手车直卖网站对其所经营的一款品牌汽车的使用年数x与销售价格y(单位:万元,辆)进行了记录整理,得到如下数据:

(I)画散点图可以看出,z与x有很强的线性相关关系,请求出z与x的线性回归方程(回归系数![]() 精确到0.01);
精确到0.01);
(II)求y关于x的回归方程,并预测某辆该款汽车当使用年数为10年时售价约为多少.
参考公式:
参考数据:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() 与
与![]() 轴相切.
轴相切.
(1)求![]() 的值;
的值;
(2)求圆M在![]() 轴上截得的弦长;
轴上截得的弦长;
(3)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作直线
作直线![]() 与圆M相切,
与圆M相切,![]() 为切点,求四边形
为切点,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)先将圆的一般方程化成标准方程,利用直线和圆相切进行求解;(2) 令![]() ,得到关于
,得到关于![]() 的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
试题解析:(1) ![]() ∵圆M:
∵圆M:![]() 与
与![]() 轴相切
轴相切
∴![]() ∴
∴![]()
(2) 令![]() ,则
,则![]() ∴
∴![]()
∴![]()
(3) ![]()
∵![]() 的最小值等于点
的最小值等于点![]() 到直线
到直线![]() 的距离,
的距离,
∴![]() ∴
∴![]()
∴四边形![]() 面积的最小值为
面积的最小值为![]() .
.
【题型】解答题
【结束】
20
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,且圆
,且圆![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,设直线
两点,设直线![]() 的方程为
的方程为![]() .
.

(1)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(2)已知直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点.
两点.
(ⅰ)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(ⅱ)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
, ![]() ,
,
是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
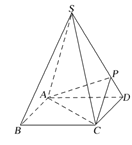
(1)求证:![]() ;
;
(2)若![]() 平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE:EC;若不存在,试说明理由.
平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE:EC;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,且
,且![]() ,
,![]() .
.
(1)证明数列![]() 为等比数列,并求出数列
为等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(3)设函数![]() (
(![]() 为常数),且(2)中的
为常数),且(2)中的![]() >
>![]() 对任意的
对任意的![]() 和
和![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com