
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
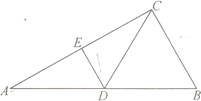

如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(1)见解析;(2)直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】
(1)在题图1中,可证![]() ,在题图2中,
,在题图2中,![]() 平面
平面![]() .进而得到
.进而得到![]() 平面
平面![]() .从而证得平面
.从而证得平面![]() 平面
平面![]() ;
;
(2)可证得![]() 平面
平面![]() .
. ![]() .则以
.则以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立如图所示的空间直角坐标系,利用空间向量可求直线
轴的正方向建立如图所示的空间直角坐标系,利用空间向量可求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:在题图1中,因为![]() ,且
,且![]() 为
为![]() 的中点.由平面几何知识,得
的中点.由平面几何知识,得![]() .
.
又因为![]() 为
为![]() 的中点,所以
的中点,所以![]()
在题图2中,![]() ,
,![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)解:因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
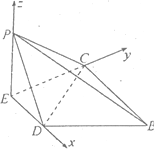
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立如图所示的空间直角坐标系
轴的正方向建立如图所示的空间直角坐标系
在题图1中,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则 ,即
,即![]()
令![]() ,则
,则![]() .所以
.所以![]() .
.
设![]() 与
与![]() 平面所成的角为
平面所成的角为![]() ,
,
则 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知某地区中小学生人数和近视情况如图1和图2所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生作为样本进行调查.

(1)求样本容量和抽取的高中生近视人数分别是多少?
(2)在抽取的![]() 名高中生中,平均每天学习时间超过9小时的人数为
名高中生中,平均每天学习时间超过9小时的人数为![]() ,其中有12名学生近视,请完成高中生平均每天学习时间与近视的列联表:
,其中有12名学生近视,请完成高中生平均每天学习时间与近视的列联表:
平均学习时间不超过9小时 | 平均学习时间超过9小时 | 总计 | |
不近视 | |||
近视 | |||
总计 |
(3)根据(2)中的列联表,判断是否有![]() 的把握认为高中生平均每天学习时间与近视有关?
的把握认为高中生平均每天学习时间与近视有关?
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣1=0与直线x﹣2y+1=0交于点P.
(Ⅰ)求过点P且平行于直线3x+4y﹣15=0的直线![]() 的方程;(结果写成直线方程的一般式)
的方程;(结果写成直线方程的一般式)
(Ⅱ)求过点P并且在两坐标轴上截距相等的直线![]() 方程(结果写成直线方程的一般式)
方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”(如下图),四个全等的直角三角形(朱实),可以围成一个大的正方形,中空部分为一个小正方形(黄实).若直角三角形中一条较长的直角边为8,直角三角形的面积为24,若在上面扔一颗玻璃小球,则小球落在“黄实”区域的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2018年10月1日起,![]() 中华人民共和国个人所得税
中华人民共和国个人所得税![]() 新规定,公民月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
新规定,公民月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3 |
超过1500元不超过4500元的部分 | 10 |
超过4500元不超过9000元的部分 | 20 |
超过9000元不超过35000元 | 25 |
|
|
![]() 如果小李10月份全月的工资、薪金为7000元,那么他应该纳税多少元?
如果小李10月份全月的工资、薪金为7000元,那么他应该纳税多少元?
![]() 如果小张10月份交纳税金425元,那么他10月份的工资、薪金是多少元?
如果小张10月份交纳税金425元,那么他10月份的工资、薪金是多少元?
![]() 写出工资、薪金收入
写出工资、薪金收入![]() 元
元![]() 月
月![]() 与应缴纳税金
与应缴纳税金![]() 元
元![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com