
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为6.
的周长为6.
(1)求椭圆![]() 的方程;
的方程;
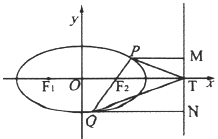
(2)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() 与
与![]() 轴的交点为
轴的交点为![]() .若四边形
.若四边形![]() 的面积是
的面积是![]() 面积的3倍,求直线
面积的3倍,求直线![]() 斜率的取值范围.
斜率的取值范围.
【答案】(1)![]() ;(2)
;(2)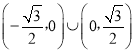 .
.
【解析】
(1)根据椭圆的离心率和焦点三角形的周长建立方程求出a,c的值即可;
(2)先设出直线PQ的方程为x=my+1,联立方程组得出根与系数关系,利用四边形PMNQ的面积是△PQT面积的3倍,得出t关于m的表达式,由t>2建立不等式,解出m的取值范围,进而根据![]() 得出k的取值范围.
得出k的取值范围.
(1)因为P是E上的点,且F1,F2为E的左、右焦点,所以|PF1|+|PF2|=2a,
又因为|F1F2|=2c,△PF1F2的周长为6,所以2a+2c=6,
又因为椭圆的离心率为![]() ,所以
,所以![]() ,解得a=2,c=1.所以
,解得a=2,c=1.所以![]() ,
,
E的方程为![]() .
.
(2)依题意,直线PQ与x轴不重合,故可设直线PQ的方程为x=my+1,
由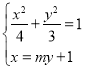 ,消去x得:(3m2+4)y2+6my-9=0,
,消去x得:(3m2+4)y2+6my-9=0,
设P(x1,y1),Q(x2,y2)则有△>0且![]() .
.
设四边形PMNQ的面积和△PQT面积的分别为S1,S2,
则S1=3S2,又因为![]() ,S2=
,S2=![]() .
.
所以![]() ,
,
即3(t-1)=2t-(x1+x2),得t=3-(x1+x2),
又x1=my1+1,x2=my2+1,于是t=3-(my1+my2+2)=1-m(y1+y2),
所以![]() ,由t>2得
,由t>2得![]() ,解得
,解得![]() ,
,
设直线PQ的斜率为k,则![]() ,所以
,所以![]() ,
,
解得![]() ,
,
所以直线PQ斜率的取值范围是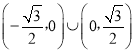 .
.


科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
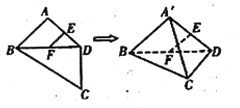
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
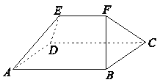
【题目】我国古代数学名著《九章算术》中记载的“刍甍”(chu meng)是指底面为矩形,顶部只有一条棱的五面体.如图,五面体![]() 是一个刍甍,其中
是一个刍甍,其中![]() 是正三角形,
是正三角形,![]() ,则以下两个结论:①
,则以下两个结论:①![]() ;②
;②![]() ,( )
,( )
A.①和②都不成立B.①成立,但②不成立
C.①不成立,但②成立D.①和②都成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当时
的图象.当时![]() ,求函数
,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2014-2018年的相关数据如下表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数 | 2 | 4 | 5 | 6 | 8 |
该产品的年利润 | 30 | 40 | 60 | 50 | 70 |
年返修台数(台) | 19 | 58 | 45 | 71 | 70 |
注:![]()
(1)从该公司2014-2018年的相关数据中任意选取3年的数据,求这3年中至少有2年生产部门考核优秀的概率.
(2)利用上表中五年的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的回归直线方程是
(万台)的回归直线方程是![]() ①.现该公司计划从2019年开始转型,并决定2019年只生产该产品1万台,且预计2019年可获利32(百万元);但生产部门发现,若用预计的2019年的数据与2014-2018年中考核优秀年份的数据重新建立回归方程,只有当重新估算的
①.现该公司计划从2019年开始转型,并决定2019年只生产该产品1万台,且预计2019年可获利32(百万元);但生产部门发现,若用预计的2019年的数据与2014-2018年中考核优秀年份的数据重新建立回归方程,只有当重新估算的![]() ,
,![]() 的值(精确到0.01),相对于①中
的值(精确到0.01),相对于①中![]() ,
,![]() 的值的误差的绝对值都不超过
的值的误差的绝对值都不超过![]() 时,2019年该产品返修率才可低于千分之一.若生产部门希望2019年考核优秀,能否同意2019年只生产该产品1万台?请说明理由.
时,2019年该产品返修率才可低于千分之一.若生产部门希望2019年考核优秀,能否同意2019年只生产该产品1万台?请说明理由.
(参考公式:![]() ,
,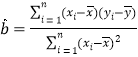
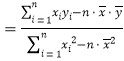 ,
,![]() ,
,![]() 相对
相对![]() 的误差为
的误差为![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,设椭圆
中,设椭圆![]() 的左焦点为
的左焦点为![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() ,且
,且![]() ,点
,点![]() 在
在![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 和圆
和圆![]() 分别相切于
分别相切于![]() ,
,![]() 两点,当
两点,当![]() 面积取得最大值时,求直线
面积取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点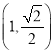 ,
,![]() 是该椭圆的左、右焦点,
是该椭圆的左、右焦点,![]() 是上顶点,且
是上顶点,且![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求![]() 的方程;
的方程;
(2)已知![]() 是坐标原点,直线
是坐标原点,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 在
在![]() 上且满足四边形
上且满足四边形![]() 是一个平行四边形,求
是一个平行四边形,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com