Question

2．已知A（-1，0），B（1，0），动点M满足∠AMB=2θ，|$\overrightarrow{AM}$|•|$\overrightarrow{BM}$|•cos²θ=3，设M的轨迹为曲线C．
（1）求曲线C的方程；
（2）过A的直线l₁与曲线C交于E、F两点，过B与l₁平行的直线l₂与曲线C交于G、H两点，求四边形EFGH的面积的最大值．

Answer 1

分析 （1）由余弦定理得|AM|²+|BM|²-2|AM||BM|cos2θ=4，及$|{\overrightarrow{AM}}|•|{\overrightarrow{BM}}|{cos^2}θ=3$得$|{\overrightarrow{AM}}|+|{\overrightarrow{BM}}|=4$，因此点M的轨迹是以A，B为焦点的椭圆；
（2）由题意得四边形EFGH是平行四边形，结合对称性得：S_EFGH=4S_OEF，设直线EF的方程为：x=my-1，E（x₁，y₁），F（x₂，y₂），由S_OEF=$\frac{1}{2}$|OA||y₁-y₂|=6$\sqrt{\frac{{m}^{2}+1}{（4+3{m}^{2}）^{2}}}$求出S_OEF的最大值即可．

解答 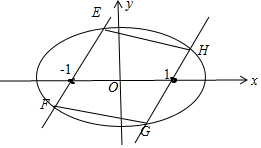解：（1）设M（x，y），在△MAB中，|AB|=1，∠AMB=2θ，
由余弦定理得|AM|²+|BM|²-2|AM||BM|cos2θ=4，
即（|AM|+|BM|）²-2|AM||BM|-2|AM||BM|cos2θ
=4（|AM|+|BM|）²-2|AM||BM|（1+cos2θ）
=4（|AM|+|BM|）²-4|AM||BM|cos²θ=4
又$|{\overrightarrow{AM}}|•|{\overrightarrow{BM}}|{cos^2}θ=3$，所以$|{\overrightarrow{AM}}|+|{\overrightarrow{BM}}|=4$，
由于$|{\overrightarrow{AM}}|+|{\overrightarrow{BM}}|=4＞2=|{AB}|$，
因此点M的轨迹是以A，B为焦点的椭圆，同时该椭圆的长半轴a=2，焦距2c=2，
所以，曲线C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$；           
（2）由题意得四边形EFGH是平行四边形，结合对称性得：
S_EFGH=4S_OEF
设直线EF的方程为：x=my-1，E（x₁，y₁），F（x₂，y₂），
把x=my-1代入方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$得（4+3m²）y²-6my-9=0
y₁+y₂=$\frac{6m}{4+3{m}^{2}}$，y₁y₂=$\frac{-9}{4+3{m}^{2}}$；且△＞0．
S_OEF=$\frac{1}{2}$|OA||y₁-y₂|=6$\sqrt{\frac{{m}^{2}+1}{（4+3{m}^{2}）^{2}}}$
令  ${m}^{2}+1=t，\\;\\;t≥1$，则S_OEF=6$\sqrt{\frac{t}{（3t+1）^{2}}}=6×\sqrt{\frac{1}{9t+\frac{1}{t}+6}}$；
又g（t）=9t+$\frac{1}{t}$在[1，+∞）递增，∴g（t）≥g（1）=10，
S_EFGH=4S_OEF≥4×6×$\frac{1}{4}$=6
∴四边形EFGH的面积的最大值为6

点评 本题考查了直线与椭圆的位置关系，及面积的最值问题，关键要掌握基本的运算技巧，属于中档题．