
 用部分自然构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行的第二个数为bn(n≥2).
用部分自然构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行的第二个数为bn(n≥2).分析 (1)由题意可得bn+1=bn+n,n≥2,运用累加法,即可得到bn;
(2)求得n≥2时,cn=$\frac{2}{n(n-1)}$=2($\frac{1}{n-1}$-$\frac{1}{n}$),运用数列的求和方法:裂项相消求和,化简整理即可得到所求和,由不等式的性质,即可得证.
解答 解:(1)由已知得b2=2,bn+1=bn+n,n≥2,
当n≥2时,b3-b2=2,b4-b3=3,…,bn-bn-1=n-1,
累加得bn-b2=2+3+…+n-1=$\frac{1}{2}$(n-2)(n+1),
则bn=1+$\frac{1}{2}$n(n-1)(n≥2);
(2)证明:由${c_1}=1,{c_n}=\frac{1}{{{b_n}-1}},({n≥2})$,
由(1)可得n≥2时,cn=$\frac{2}{n(n-1)}$=2($\frac{1}{n-1}$-$\frac{1}{n}$),
前n项和为Tn=1+2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$)
=1+2(1-$\frac{1}{n}$)=3-$\frac{2}{n}$<3.
点评 本题考查数列的递推关系和通项公式的求法,注意运用累加法,考查数列的求和方法:裂项相消求和,考查运算能力,属于中档题.


科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:解答题
设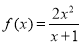 ,
,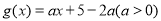 .
.
(1)求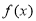 在
在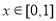 上的值域;
上的值域;
(2)若对于任意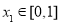 ,总存在
,总存在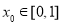 ,使得
,使得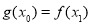 成立,求
成立,求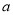 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=x+\frac{4}{x}$ | B. | $y=lg(x+1)+\frac{1}{lg(x+1)}$ | ||
| C. | $y=\sqrt{{x^2}+1}+\frac{1}{{\sqrt{{x^2}+1}}}$ | D. | $y=sinx+\frac{1}{sinx},({0<x<\frac{π}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com