
【题目】若![]() 是一个集合,
是一个集合,![]() 是一个以
是一个以![]() 的某些子集为元素的集合,且满足:(1)
的某些子集为元素的集合,且满足:(1)![]() 属于
属于![]() ,
,![]() 属于
属于![]() ;(2)
;(2)![]() 中任意多个元素的并集属于
中任意多个元素的并集属于![]() ;(3)
;(3)![]() 中任意多个元素的交集属于
中任意多个元素的交集属于![]() ,则称
,则称![]() 是集合
是集合![]() 上的一个拓补.已知集合
上的一个拓补.已知集合![]() ,对于下面给出的四个集合
,对于下面给出的四个集合![]() :
:
①![]() ②
②![]()
③![]() ④
④![]()
其中是集合![]() 上的拓补的集合
上的拓补的集合![]() 的序号是______.(写出所有的拓补的集合
的序号是______.(写出所有的拓补的集合![]() 的序号)
的序号)
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在非零常数
,如果存在非零常数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为
的“似周期”为![]() ,那么它是周期为
,那么它是周期为![]() 的周期函数;
的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③函数![]() 是“似周期函数”;
是“似周期函数”;
④如果函数![]() 是“似周期函数”,那么“
是“似周期函数”,那么“![]() ,
,![]() ”.
”.
其中是真命题的序号是___________.(写出所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为p,公差为
的首项为p,公差为![]() ,对于不同的自然数
,对于不同的自然数![]() ,直线
,直线![]() 与
与![]() 轴和指数函数
轴和指数函数![]() 的图象分别交于点
的图象分别交于点![]() 与
与![]() (如图所示),记
(如图所示),记![]() 的坐标为
的坐标为![]() ,直角梯形
,直角梯形![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,一般地记直角梯形
,一般地记直角梯形![]() 的面积为
的面积为![]() .
.

(1)求证:数列![]() 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;
(2)设![]() 的公差
的公差![]() ,是否存在这样的正整数
,是否存在这样的正整数![]() ,构成以
,构成以![]() ,
,![]() ,
,![]() 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;
(3)设![]() 的公差
的公差![]() 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列![]() 各项的和
各项的和![]() ?并请说明理由.
?并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,在同一个坐标系中,
,在同一个坐标系中,![]() 及
及![]() 的部分图象如图所示,则( ).
的部分图象如图所示,则( ).

A. 当![]() 时,
时,![]() 取得最大值 B. 当
取得最大值 B. 当![]() 时,
时,![]() 取得最大值
取得最大值
C. 当![]() 时,
时,![]() 取得最小值 D. 当
取得最小值 D. 当![]() 时,
时,![]() 取得最小值
取得最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
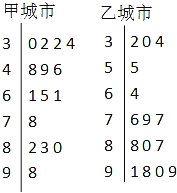
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个国际象棋棋盘(由8×8个方格组成),其中有一个小方格因破损而被剪去(破损位置不确定).“L”形骨牌由三个相邻的小方格组成,如图所示.现要将这个破损的棋盘剪成数个“L”形骨牌,则( )
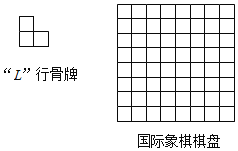
A.至多能剪成19块“L”形骨牌
B.至多能剪成20块“L”形骨牌
C.最多能剪成21块“L”形骨牌
D.前三个答案都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足:a1=![]() ,a2=
,a2=![]() ,且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立,则
,且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立,则![]() 的值为( )
的值为( )
A. 5032 B. 5044 C. 5048 D. 5050
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com