分析:(Ⅰ)由题意,对函数求导得到f'(x)=x
2-2x=x(x-2),可得出当t=3时,f(x)在(-1,0),(2,3)上递增,在(0,2)上递减,由此函数的最值与单调区间易求得;
(II)解法一:由题意函数
g(t)=(t-2)2,t>-1.记方程f'(x)=g(t),可得出
x2-2x=(t-2)2,由于方程f'(x)=g(t)的解为x
0,x
0∈(-1,t),故可构造函数
p(x)=x2-2x-(t-2)2在x
0∈(-1,t),分类讨论x
0的个数;
解法二:可作出两函数f'(x)=x
2-2x与
g(t)=(t-2)2,t>-1的图象,由图象对t的取值范围分类讨论得出每一种情况下两个函数图象的交点个数即可得到x
0的个数.
解答:解:(Ⅰ)因为f'(x)=x
2-2x=x(x-2)…(1分)
由f'(x)>0⇒x>2或x<0;由f'(x)<0⇒0<x<2,
所以当t=3时,f(x)在(-1,0),(2,3)上递增,在(0,2)上递减 …(3分)
因为
f(-1)=,f(0)=3,
f(2)=-4+3=,f(3)=3,
所以当x=-1或2时,函数f(x)取最小值
f(-1)=,…(5分)
当x=0或3时,函数f(x)取最大值f(0)=3,…(6分)
(Ⅱ)解法1:因为f'(x)=x
2-2x,所以
x2-2x=(t-2)2,
令
p(x)=x2-2x-(t-2)2,
因为
p(-1)=3-(t-2)2=-(t+1)(t-5),
p(t)=t(t-2)-(t-2)2=(t+1)(t-2),…(9分)
所以①当t>5或-1<t<2时,p(-2)•p(t)<0,所以p(x)=0在(-2,t)上有且只有一解…(11分)
②当2<t<5时,p(-2)>0且p(t)>0,但由于
p(0)=-(t-2)2<0,
所以p(x)=0在(-2,t)上有两解 …(13分)
③当t=2时,p(x)=x
2-2x=0⇒x=0或x=2,所以p(x)=0在(-2,t)上有且只有一解x=0;
当t=5时,p(x)=x
2-2x-3=0⇒x=-1或x=3,
所以p(x)=0在(-1,5)上也有且只有一解x=3…(14分)
综上所述,当t≥5或-1<t≤2时,有唯一的x
0适合题意;当2<t<5时,有两个x
0适合题意.…(15分)
解法2:画出f'(x)=x
2-2x与
g(t)=(t-2)2,t>-1的图象,
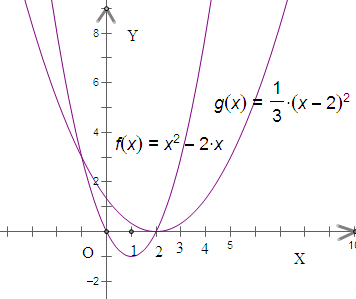
(1)当-1<t≤0时,两图象有一个交点,有唯一的x
0适合题意;-------------(8分)
(2)当0<t≤2时,
0≤(t-2)2<,此时两图象有一个交点,有唯一的x
0适合题意;-------------(10分)
(3)当2<t<5时,因为f'(-1)=f'(3)=3,
(t-2)2=3得到t
1=-1,t
2=5,
0<(t-2)2<3,此时两图象有两个交点,有两个x
0适合题意;------(12分)
(4)当t=2或t=5时,当t=2时,p(x)=x
2-2x=0⇒x=0或x=2,所以p(x)=0在(-2,t)上有且只有一解x=0;
当t=5时,p(x)=x
2-2x-3=0⇒x=-1或x=3
0<(t-2)2<3,
此时两图象有两个交点,有两个x
0适合题意;---------------------(14分)
综上所述,当t≥5或-1<t≤2时,有唯一的x
0适合题意;
当2<t<5时,有两个x
0适合题意.…(15分)

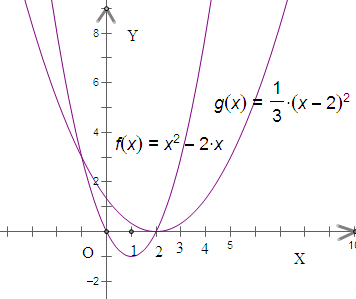


 名校课堂系列答案
名校课堂系列答案