
| A. | $\sqrt{5}$:(2+$\sqrt{5}$) | B. | 2:(2+$\sqrt{5}$) | C. | 1:(1+$\sqrt{5}$) | D. | $\sqrt{5}$:(1+$\sqrt{5}$) |
分析 由x2=8y的焦点为F(0,2),点A坐标为A(-1,0),直线AF的斜率为k=2,过M作MP⊥l于P,根据抛物线物定义得:|FM|=|PM|,$\frac{丨MP丨}{丨NP丨}$=2,可得|MP|=2|NP|,由勾股定理可知:|MN|=$\sqrt{丨MP{丨}^{2}+丨NP{丨}^{2}}$=$\sqrt{5}$|NP|,|FN|=|MN|+|MF|=|MN|+|MP|=(2+$\sqrt{5}$)|NP|,即可求得|MN|:|FN|的值.
解答 解:∵抛物线C:x2=8y的焦点为F(0,2),点A坐标为A(-1,0),
∴抛物线的准线方程为l:y=-2,直线AF的斜率为k=2,
过M作MP⊥l于P,根据抛物线物定义得:|FM|=|PM|,
∵Rt△MPN中,tan∠MNP=k=2,
∴$\frac{丨MP丨}{丨NP丨}$=2,可得|MP|=2|NP|,
则|MN|=$\sqrt{丨MP{丨}^{2}+丨NP{丨}^{2}}$=$\sqrt{5}$|NP|,
而|FN|=|MN|+|MF|=|MN|+|MP|=(2+$\sqrt{5}$)|NP|,
∴|MN|:|FN|=$\sqrt{5}$:(2+$\sqrt{5}$),
故选A.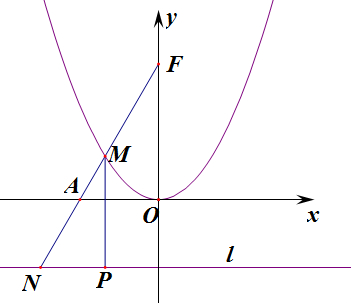
点评 本题考查抛物线的性质,直线的斜率公式,勾股定理,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{16}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
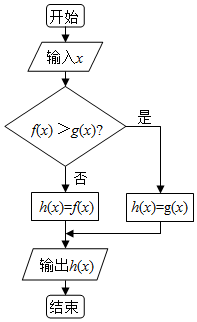
| A. | 2016 | B. | 2017 | C. | logπ2016 | D. | ln2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{2}+{y^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com