
【题目】已知直线![]() 过定点
过定点![]() ,圆
,圆![]() .在圆
.在圆![]() 上任取一点P,连接
上任取一点P,连接![]() ,在
,在![]() 上取点M,使得
上取点M,使得![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(1)求点M的轨迹方程;
(2)过点![]() 的直线
的直线![]() 与点M的轨迹交于A,B两点,O为坐标原点,求
与点M的轨迹交于A,B两点,O为坐标原点,求![]() 面积的最大值.
面积的最大值.
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】下表为2016年至2019年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 | 1 | 2 | 3 | 4 |
线下销售额 | 95 | 165 | 230 | 310 |
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该百货零售企业的线下销售额;
的线性回归方程,并预测2020年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了55位男顾客、50位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有10人、女顾客有20人,能否在犯错误的概率不超过0.025的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
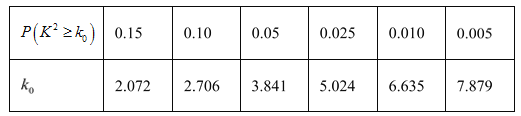
参考公式及数据:
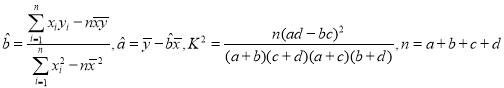 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知6名某疾病病毒密切接触者中有1名感染病毒,其余5名健康,需要通过化验血液来确定感染者.血液化验结果呈阳性的即为感染者,呈阴性即为健康.
(1)若从这6名密切接触者中随机抽取3名,求抽到感染者的概率;
(2)血液化验确定感染者的方法有:①逐一化验;②分组混合化验:先将血液分成若干组,对组内血液混合化验,若化验结果呈阴性,则该组血液不含病毒;若化验结果呈阳性,则对该组的备份血液逐一化验,直至确定感染者.
(i)采取逐一化验,求所需检验次数![]() 的数学期望;
的数学期望;
(ii)采取平均分组混合化验(每组血液份数相同),依据所需化验总次数的期望,选择合理的平均分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角A,B,C所对的边分别是a,b,c,其面积S
的内角A,B,C所对的边分别是a,b,c,其面积S![]() .
.
(1)若a![]() ,b
,b![]() ,求cosB.
,求cosB.
(2)求sin(A+B)+sinBcosB+cos(B﹣A)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com