
| A. | [$\frac{1}{2}$,1] | B. | (-∞,-2) | C. | [-$\frac{5}{2}$,4] | D. | [-2,$\frac{7}{2}$] |
分析 由x=$\frac{4π}{3}$时f(x)取得最大值1,从而有8ω=12k+4,k∈Z,又由题意可得$\frac{T}{2}$≥$\frac{4π}{3}$且$\frac{T}{2}$≥$\frac{2π}{3}$,可得0<ω≤$\frac{3}{4}$,从而可求ω的值;令t=$\frac{1}{2}$x-$\frac{π}{6}$,可求f(x)的值域为[$\frac{1}{2}$,1],由题意可得$\left\{\begin{array}{l}{m-3≤\frac{1}{2}}\\{m+3≥1}\end{array}\right.$,从而解得实数m的取值范围.
解答 解:由已知条件知,x=$\frac{4π}{3}$时f(x)取得最大值1,
从而有ω•$\frac{4π}{3}$-$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,即8ω=12k+4,k∈Z,
又由题意可得该函数的最小正周期T满足:$\frac{T}{2}$≥$\frac{4π}{3}$且$\frac{T}{2}$≥$\frac{2π}{3}$,
于是有T≥$\frac{8π}{3}$,0<ω≤$\frac{3}{4}$,满足0<12k+4≤6的正整数k的值为0,
于是ω=$\frac{1}{2}$,
令t=$\frac{1}{2}$x-$\frac{π}{6}$,因为x∈[π,2π],得t∈[$\frac{π}{3}$,$\frac{5π}{6}$],
由y=sint,t∈[$\frac{π}{3}$,$\frac{5π}{6}$],
得y∈[$\frac{1}{2}$,1],即f(x)的值域为[$\frac{1}{2}$,1],
由于x∈[π,2π]时,不等式m-3≤f(x)≤m+3恒成立,
故有$\left\{\begin{array}{l}{m-3≤\frac{1}{2}}\\{m+3≥1}\end{array}\right.$,
解得-2≤m$\frac{7}{2}$,
即m的取值范围是[-2,$\frac{7}{2}$].
故选:D.
点评 本题主要考查了正弦函数的周期性和复合函数的值域,考查不等式恒成立问题的解法,考查了不等式的解法,以及推理和判断能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{5}$ | B. | $3+\sqrt{5}$ | C. | $14+6\sqrt{5}$ | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{13}{20}$ | C. | $\frac{54}{125}$ | D. | $\frac{27}{125}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
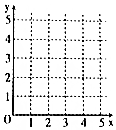 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如表所示:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如表所示:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(h) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
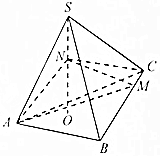 如图在三棱锥S-ABC中,CA=CB=3,∠ACB=30°,高SO=8,动点M、N分别在线段BC上SO上,且SN=2CM=2x,则下列四个图象中大致描绘了四面体AMCN的体积V与x变化关系(其中x∈(0,3])的是( )
如图在三棱锥S-ABC中,CA=CB=3,∠ACB=30°,高SO=8,动点M、N分别在线段BC上SO上,且SN=2CM=2x,则下列四个图象中大致描绘了四面体AMCN的体积V与x变化关系(其中x∈(0,3])的是( )| A. | 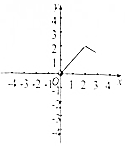 | B. | 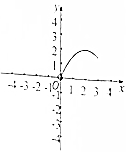 | C. | 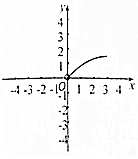 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com