
【题目】下列说法正确的是( )
A.在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B.某地气象局预报:6月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
C.回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图,给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出![]() 的值为( )
的值为( )
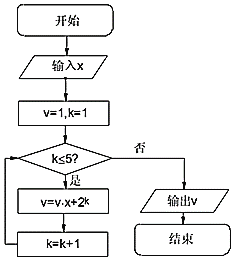
A.80B.192C.448D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】闰月年指农历里有闰月的年份,比如2020年是闰月年,4月23日至5月22日为农历四月,5月23日至6月20日为农历闰四月.农历置闰月是为了农历年的平均长度接近回归年:农历年中的朔望月的平均长度为29.5306日,![]() 日,回归年的总长度为365.2422日,两者相差10.875日.因此,每19年相差206.625日,约等于7个朔望月.这样每19年就有7个闰月年.以下是1640年至1694年间所有的闰月年:
日,回归年的总长度为365.2422日,两者相差10.875日.因此,每19年相差206.625日,约等于7个朔望月.这样每19年就有7个闰月年.以下是1640年至1694年间所有的闰月年:
1640 | 1642 | 1645 | 1648 | 1651 | 1653 | 1656 |
1659 | 1661 | 1664 | 1667 | 1670 | 1672 | 1675 |
1678 | 1680 | 1 683 | 1686 | 1689 | 1691 | 1694 |
则从2020年至2049年,这30年间闰月年的个数为( )
A.10B.11C.12D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() ,
,![]() 是正三角形,且平面
是正三角形,且平面![]() 平面ABC,
平面ABC,![]() ,E,G分别为AB,BC的中点.
,E,G分别为AB,BC的中点.

(Ⅰ)证明:![]() 平面ABD;
平面ABD;
(Ⅱ)若F是线段DE的中点,求AC与平面FGC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆![]() 的右焦点,点A为椭圆的右顶点.
的右焦点,点A为椭圆的右顶点.
(1)求过点F、A且和直线![]() 相切的圆C的方程;
相切的圆C的方程;
(2)过点F任作一条不与![]() 轴重合的直线
轴重合的直线![]() ,直线
,直线![]() 与椭圆交于P,Q两点,直线PA,QA分别与直线
与椭圆交于P,Q两点,直线PA,QA分别与直线![]() 相交于点M,N.试证明:以线段MN为直径的圆恒过点F.
相交于点M,N.试证明:以线段MN为直径的圆恒过点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,我国老年人口比例不断上升,造成日趋严峻的人口老龄化问题.2019年10月12日,北京市老龄办、市老龄协会联合北京师范大学中国公益研究院发布《北京市老龄事业发展报告(2018)》,相关数据有如下图表.规定年龄在15岁至59岁为“劳动年龄”,具备劳动力,60岁及以上年龄为“老年人”,据统计,2018年底北京市每2.4名劳动力抚养1名老年人.
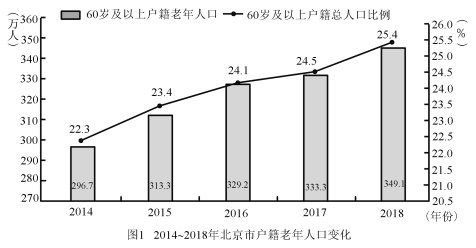
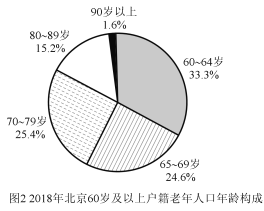
(Ⅰ)请根据上述图表计算北京市2018年户籍总人口数和北京市2018年的劳动力数;(保留两位小数)
(Ⅱ)从2014年起,北京市老龄人口与年份呈线性关系,比照2018年户籍老年人人口年龄构成,预计到2020年年底,北京市90以上老人达到多少人?(精确到1人)
(附:对于一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: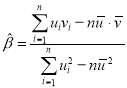 ,
,![]() .
.![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间![]() 岁之间,对区间
岁之间,对区间![]() 岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:

组数 | 分组 | 人数 |
第一组 |
| 2 |
第二组 |
| a |
第三组 |
| 5 |
第四组 |
| 4 |
第五组 |
| 3 |
第六组 |
| 2 |
(1)求a的值并画出频率分布直方图;
(2)从被调查的20人且年龄在![]() 岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间
岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间![]() 岁年龄段的人数为X,求随机变量X的分布列及数学期望.
岁年龄段的人数为X,求随机变量X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,上顶点为点
,上顶点为点![]() ,若
,若![]() 是面积为
是面积为![]() 的等边三角形.
的等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,求使
,求使![]() 的面积最大时直线
的面积最大时直线![]() 的方程(
的方程(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com