
分析 通过记Q(4,2)可知k=$\frac{y-2}{x-4}$即为过椭圆上点P与点Q的直线的斜率,通过联立直线PQ与椭圆方程并令△=0,进而计算即得结论.
解答 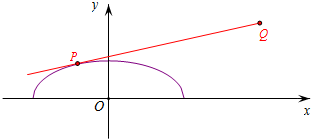 解:记Q(4,2),k=$\frac{y-2}{x-4}$,则所求值k即为过椭圆上点P与点Q的直线的斜率,
解:记Q(4,2),k=$\frac{y-2}{x-4}$,则所求值k即为过椭圆上点P与点Q的直线的斜率,
易知直线PQ的方程为:y=kx+2-4k,并与椭圆方程联立,
消去x整理得:(4k2+1)x2-16k(2k-1)x+16(2k-1)2-4=0,
要使k最小,只需上述方程只有唯一一个解,
即△=[-16k(2k-1)]2-4(4k2+1)[16(2k-1)2-4]=0,
化简得:12k2-16k+3=0,
解得:k=$\frac{4+\sqrt{7}}{6}$(舍)或k=$\frac{4-\sqrt{7}}{6}$,
故答案为:$\frac{4-\sqrt{7}}{6}$.
点评 本题考查椭圆的简单性质,考查数形结合能力,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com