
【题目】已知曲线 ![]() 的参数方程
的参数方程 ![]() (
( ![]() 为参数),曲线
为参数),曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)将曲线 ![]() 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线 ![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)试问曲线 ![]() ,
, ![]() 是否相交?若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交?若相交,请求出公共弦的长;若不相交,请说明理由.
科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 . 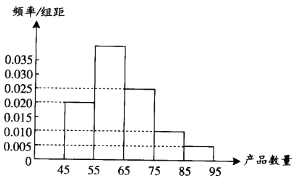
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.
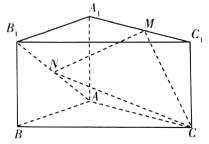
(I)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(II)若点![]() 为
为![]() 的中点且
的中点且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
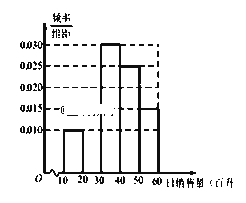
【题目】某加油站20名员工日销售量的频率分布直方图,如图所示:
(1)补全该频率分布直方图在[20,30)的部分,并分别计算日销售量在 [10,20),[20,30)的员工数;
(2)在日销量为[10,30)的员工中随机抽取2人,求这两名员工日销量在 [20,30)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是____________.
【答案】![]()
【解析】∵圆C的方程可化为(x-4)2+y2=1,∴圆C的圆心为(4,0),半径为1.由题意知,直线y=kx-2上至少存在一点A(x0,kx0-2),以该点为圆心,1为半径的圆与圆C有公共点,∴存在x0∈R,使得AC≤1+1成立,即ACmin≤2.
∵ACmin即为点C到直线y=kx-2的距离![]() ,
,
∴![]() ≤2,解得0≤k≤
≤2,解得0≤k≤![]() .∴k的最大值是
.∴k的最大值是![]() .
.
【题型】填空题
【结束】
15
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() .
.
(1)若直线![]() 与直线
与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(2)若![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,已知
上,已知![]() 的中点在
的中点在![]() 轴上,求点
轴上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办校园科技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知A、B两学习小组各有5位同学,每位同学在两场讲座任意选听一场.若A组1人选听《生活趣味数学》,其余4人选听《校园舞蹈赏析》;B组2人选听《生活趣味数学》,其余3人选听《校园舞蹈赏析》.
(1)若从此10人中任意选出3人,求选出的3人中恰有2人选听《校园舞蹈赏析》的概率;
(2)若从A、B两组中各任选2人,设X为选出的4人中选听《生活趣味数学》的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体中, ![]() 菱形,
菱形, ![]() 是矩形,
是矩形, ![]() ⊥平面
⊥平面 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)异面直线 ![]() 与
与 ![]() 所成的角余弦值;
所成的角余弦值;
(Ⅱ)求证平面 ![]() ⊥平面
⊥平面 ![]() ;
;
(Ⅲ)在线段 ![]() 取一点
取一点 ![]() ,当二面角
,当二面角 ![]() 的大小为60°时,求
的大小为60°时,求 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com