【题目】为了解某班学生喜好体育运动是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否，采用分层抽样法抽取容量为10的样本，则抽到喜好体育运动的人数为6.
（1）请将上面的列联表补充完整；
（2）能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关？说明理由.
附：
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
小学生10分钟应用题系列答案
目标测试系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，离心率
，且椭圆的短轴长为2.
（1）球椭圆的标准方程；
（2）已知直线
过右焦点
，且它们的斜率乘积为
，设分别与椭圆交于点
和
.
①求
的值；
②设
的中点
，
的中点为，求
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A. 某厂一批产品的次品率为
，则任意抽取其中10件产品一定会发现一件次品
B. 掷一枚硬币，连续出现5次正面向上，第六次出现反面向上的概率与正面向上的概率仍然都为0.5
C. 某医院治疗一种疾病的治愈率为10%，那么前9个病人都没有治愈，第10个人就一定能治愈
D. 气象部门预报明天下雨的概率是90%，说明明天该地区90%的地方要下雨，其余10%的地方不会下雨
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，过抛物线
（
）上一点
，作两条直线分别交抛物线于点
，
，若
与
的斜率满足
.
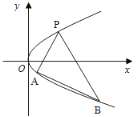
（1）证明：直线
的斜率为定值，并求出该定值；
（2）若直线在
轴上的截距
，求
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
为椭圆
上一点，
分别为
关于
轴，原点，
轴的对称点，
（1）求四边形
面积的最大值；
（2）当四边形最大时，在线段
上任取一点
，若过的直线与椭圆相交于
两点，且
中点恰为，求直线斜率
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题：
①若A、B、C、D是空间任意四点，则有
；
②
是
、
共线的充要条件；
③对空间任意一点P与不共线的三点A、B、C，若
，（
，y，z∈R），则P、A、B、C四点共面．
其中不正确命题的个数是（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线C1的渐近线是
x±2y=0，焦点坐标是F1（-
，0）、F2（，0）．
（1）求双曲线C1的方程；
（2）若椭圆C2与双曲线C1有公共的焦点，且它们的离心率之和为
，点P在椭圆C2上，且|PF1|=4，求∠F1PF2的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．
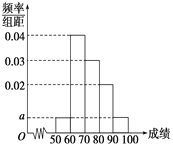
(1)求图中a的值；
(2)根据频率分布直方图，估计这100名学生语文成绩的平均分；
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
（
），
.
（1）若曲线
与
在它们的交点
处有相同的切线，求实数
，
的值；
（2）当
时，若函数
在区间
内恰有两个零点，求实数a的取值范围；
（3）当
，
时，求函数
在区间
上的最小值.
[选修4-4：坐标系与参数方程]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
