
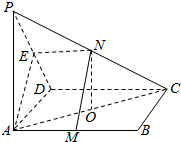
 如图,己知P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,O是AC的中点.
如图,己知P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,O是AC的中点.分析 (1)由已知推导出四边形AMNE是平行四边形,由此能证明MN∥平面PAD.
(2)连接MO,NO,推导出∠MNO就是PA与MN所成的角,由此能求出异面直线PA与MN所成的角的大小.
解答 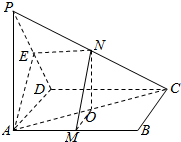 证明:(1)∵P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,
证明:(1)∵P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,
∴EN∥CD,EN=$\frac{1}{2}CD$,AM∥CD,AM=$\frac{1}{2}CD$,
∴EN$\underset{∥}{=}$AM,
∴四边形AMNE是平行四边形,
∴MN∥AE,
∵AE?平面PAD,MN?平面PAD,
∴MN∥平面PAD.
解:(2)连接MO,NO,
∵MN=BC=4,PA=4$\sqrt{3}$,∴MO=$\frac{1}{2}BC$=2,NO$\underset{∥}{=}$$\frac{1}{2}$PA=2$\sqrt{3}$,
∴∠MNO就是PA与MN所成的角,
在△MNO中,由余弦定理得cos∠MNO=$\frac{16+12-4}{2×4×2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠MNO=30°.
∴异面直线PA与MN所成的角的大小为30°.
点评 本题考查线面平行的证明,考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{2}$) | B. | (-$\frac{π}{2}$,$\frac{π}{2}$) | C. | (-π,0) | D. | (0,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
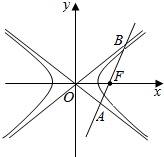 如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为11,12,经过右焦点F垂直于11的直线分别交11,12于A,B两点,若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,则该双曲线的离心率为( )
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为11,12,经过右焦点F垂直于11的直线分别交11,12于A,B两点,若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,则该双曲线的离心率为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
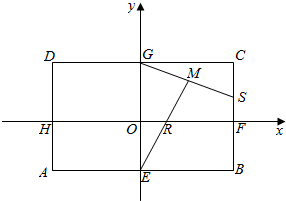 矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.
矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 所有的质数都是奇数 | B. | ?x∈R,2x2+2≥2 | ||
| C. | 对每一个无理数x,x2也是无理数 | D. | 所有长度相等的向量均相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 455 068 047 447 176 | B. | 169 105 071 286 443 | ||
| C. | 050 358 074 439 332 | D. | 447 176 335 025 212 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com