
ЎҫМвДҝЎҝ¶ФДіРЈёЯ¶юДкј¶С§ЙъІОјУЙзЗш·юОсҙОКэҪшРРНіјЖЈ¬Лж»ъійИЎMГыС§ЙъЧчОӘСщұҫЈ¬өГөҪХвMГыС§ЙъІОјУЙзЗш·юОсөДҙОКэЈ®ёщҫЭҙЛКэҫЭЧчіцБЛЖөКэУлЖөВКөДНіјЖұнәНЖөВК·ЦІјЦұ·ҪНјИзПВЈә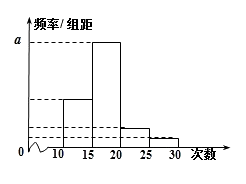

ЈЁ1Ј©ЗуіцұнЦРMЈ¬Pј°НјЦР ![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©ИфёГРЈёЯ¶юС§ЙъУР240ИЛЈ¬КФ№АјЖёГРЈёЯ¶юС§ЙъІОјУЙзЗш·юОсөДҙОКэФЪЗшјд[10,15]ДЪөДИЛКэЈ»
ЈЁ3Ј©ФЪЛщИЎСщұҫЦРЈ¬ҙУІОјУЙзЗш·юОсөДҙОКэІ»ЙЩУЪ20ҙОөДС§ЙъЦРИОСЎ2ИЛЈ¬ЗуЦБ¶аТ»ИЛІОјУЙзЗш·юОсҙОКэФЪЗшјд[25,30]ДЪөДёЕВКЈ®
Ўҫҙр°ёЎҝ
ЈЁ1Ј©ҪвЈәУЙ·ЦЧй ![]() ДЪөДЖөКэКЗ
ДЪөДЖөКэКЗ ![]() Ј¬ЖөВККЗ
Ј¬ЖөВККЗ ![]() ЦӘЈ¬
ЦӘЈ¬ ![]() Ј¬ЛщТФ
Ј¬ЛщТФ ![]()
ТтОӘЖөКэЦ®әНОӘ ![]() Ј¬ЛщТФ
Ј¬ЛщТФ ![]() Ј¬
Ј¬ ![]() .
.![]()
ТтОӘ ![]() КЗ¶ФУҰ·ЦЧй
КЗ¶ФУҰ·ЦЧй ![]() өДЖөВКУлЧйҫаөДЙМЈ¬ЛщТФ
өДЖөВКУлЧйҫаөДЙМЈ¬ЛщТФ ![]()
ЈЁ2Ј©ҪвЈәТтОӘёГРЈёЯИэС§ЙъУР240ИЛЈ¬·ЦЧй ![]() ДЪөДЖөВККЗ
ДЪөДЖөВККЗ ![]() Ј¬
Ј¬
ЛщТФ№АјЖёГРЈёЯИэС§ЙъІОјУЙзЗш·юОсөДҙОКэФЪҙЛЗшјдДЪөДИЛКэОӘ60ИЛ
ЈЁ3Ј©ҪвЈәХвёцСщұҫІОјУЙзЗш·юОсөДҙОКэІ»ЙЩУЪ20ҙОөДС§Йъ№ІУР ![]() ИЛЈ¬
ИЛЈ¬
ЙиФЪЗшјд ![]() ДЪөДИЛОӘ
ДЪөДИЛОӘ ![]() Ј¬ФЪЗшјд
Ј¬ФЪЗшјд ![]() ДЪөДИЛОӘ
ДЪөДИЛОӘ ![]() .
.
ФтИОСЎ ![]() ИЛ№ІУР
ИЛ№ІУР ![]()
![]() Ј¬
Ј¬ ![]() 15ЦЦЗйҝцЈ¬
15ЦЦЗйҝцЈ¬
¶шБҪИЛ¶јФЪ ![]() ДЪЦ»ДЬКЗ
ДЪЦ»ДЬКЗ ![]() Т»ЦЦ
Т»ЦЦ
ЛщТФЛщЗуёЕВКОӘ ![]() .ЈЁФјОӘ
.ЈЁФјОӘ ![]() Ј©
Ј©
ЎҫҪвОцЎҝ(1)ёщҫЭЖөВКЈ¬ЖөКэәНСщұҫИЭБҝөД№ШПөјҙЖөВКөИУЪЖөКэіэТФСщұҫИЭБҝЈ¬ФЩёщҫЭТСЦӘөДКэЦөјҙҝЙЗуіцMЎўpәНaөДЦөЎЈ(2)УЙЖөВКәНЖөКэөДНіјЖұнҝЙЦӘЈ¬ёЯ¶юС§ЙъУРІОјУЙзЗш·юОсөДҙОКэФЪЗшјд[10,15]ДЪөДЖөВКОӘ0.25Ј¬УЙҙЛДЬ№АјЖіцёГРЈёЯ¶юС§ЙъІОјУЙзЗш·юОсөДҙОКэФЪЗшјдДЪөДИЛКэОӘ60ИЛЎЈ(3)УЙМвТвХвёцСщұҫЦРЈ¬ІОјУЙзЗш·юОсөДҙОКэІ»ЙЩУЪ20ҙОөДС§Йъ№ІУР6ИЛЈ¬ҪбәПМвТвБРҫЩіцЛщУРКВјюәНВъЧгМхјюөДКВјюЈ¬УЙ¶ФБўКВјюөДёЕВКЗуіцҪб№ыЎЈ


 »Ҙ¶ҜҝОМГПөБРҙр°ё
»Ҙ¶ҜҝОМГПөБРҙр°ё јӨ»оЛјО¬ЦЗДЬСөБ·ҝОКұөјС§Б·ПөБРҙр°ё
јӨ»оЛјО¬ЦЗДЬСөБ·ҝОКұөјС§Б·ПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЦұҪЗЧшұкПөxOyЦРЈ¬ТСЦӘөгAЈЁ0Ј¬3Ј©әНBЈЁ6Ј¬0Ј©Ј®
ЈЁўсЈ©ЗуПЯ¶ОABҙ№ЦұЖҪ·ЦПЯөД·ҪіМЈ»
ЈЁўтЈ©ИфЗъПЯCЙПөДИОТвТ»өгPВъЧг2|PA|ЈҪ|PB|Ј¬ЗуЗъПЯCөД·ҪіМЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиәҜКэy=fЎеЈЁxЈ©КЗy=fЎдЈЁxЈ©өДөјКэЈ®ДіН¬С§ҫӯ№эМҪҫҝ·ўПЦЈ¬ИОТвТ»ёцИэҙОәҜКэfЈЁxЈ©=ax3+bx2+cx+dЈЁaЎЩ0Ј©¶јУР¶ФіЖЦРРДЈЁx0 Ј¬ fЈЁx0Ј©Ј©Ј¬ЖдЦРx0ВъЧгfЎеЈЁx0Ј©=0Ј®ТСЦӘәҜКэfЈЁxЈ©= ![]() x3©Ғ
x3©Ғ ![]() x2+3x©Ғ
x2+3x©Ғ ![]() Ј¬ФтfЈЁ
Ј¬ФтfЈЁ ![]() Ј©+fЈЁ
Ј©+fЈЁ ![]() Ј©+fЈЁ
Ј©+fЈЁ ![]() Ј©+Ўӯ+fЈЁ
Ј©+Ўӯ+fЈЁ ![]() Ј©= Ј®
Ј©= Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЕЧОпПЯy2ЈҪ4xөДДЪҪУИэҪЗРОөДТ»ёц¶ҘөгФЪФӯөгЈ¬ИэұЯЙПөДёЯПЯ¶јНЁ№эЕЧОпПЯөДҪ№өгЈ¬ЗуҙЛИэҪЗРОНвҪУФІөД·ҪіМЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ ![]() ЗТ
ЗТ ![]() .
.
ЈЁ1Ј©өұ ![]() КұЈ¬ЗуәҜКэ
КұЈ¬ЗуәҜКэ ![]() өДөҘөчЗшјдәНј«ЦөЈ»
өДөҘөчЗшјдәНј«ЦөЈ»
ЈЁ2Ј©ЗуәҜКэ ![]() ФЪЗшјд
ФЪЗшјд ![]() ЙПөДЧоРЎЦө.
ЙПөДЧоРЎЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҪьЖЪЎ°№ІПнөҘіөЎұФЪИ«№ъ¶аёціЗКРіЦРшЙэОВЈ¬ДіТЖ¶Ҝ»ҘБӘНш»ъ№№НЁ№э¶ФК№УГХЯөДөчІйөГіцЈ¬ПЦФЪКРіЎЙПіЈјыөД°ЛёцЖ·ЕЖөДЎ°№ІПнөҘіөЎұөДВъТв¶ИЦёКэИзҫҘТ¶НјЛщКҫЈә
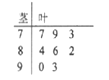
ЈЁўсЈ©ЗуіцХвЧйКэҫЭөДЖҪҫщКэәНЦРО»КэЈ»
ЈЁўтЈ©ДіУГ»§ҙУВъТв¶ИЦёКэі¬№э80өДЖ·ЕЖЦРЛж»ъСЎФсБҪёцЖ·ЕЖК№УГЈ¬ЗуЛщСЎБҪёцЖ·ЕЖөДВъТв¶ИЦёКэҫщі¬№э85өДёЕВК.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ ![]() өДТ»ёцҪ№өгУлЕЧОпПЯ
өДТ»ёцҪ№өгУлЕЧОпПЯ ![]() өДҪ№өг
өДҪ№өг ![]() ЦШәПЈ¬ЗТөг
ЦШәПЈ¬ЗТөг ![]() өҪЦұПЯ
өҪЦұПЯ ![]() өДҫаАлОӘ
өДҫаАлОӘ ![]() Ј¬
Ј¬ ![]() Ул
Ул ![]() өД№«№ІПТіӨОӘ
өД№«№ІПТіӨОӘ ![]() .
.
ЈЁ1Ј©ЗуНЦФІ ![]() өД·ҪіМј°өг
өД·ҪіМј°өг ![]() өДЧшұкЈ»
өДЧшұкЈ»
ЈЁ2Ј©№эөг ![]() өДЦұПЯ
өДЦұПЯ ![]() Ул
Ул ![]() Ҫ»УЪ
Ҫ»УЪ ![]() БҪөгЈ¬Ул
БҪөгЈ¬Ул ![]() Ҫ»УЪ
Ҫ»УЪ ![]() БҪөгЈ¬Зу
БҪөгЈ¬Зу ![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ҫШРОABCDЦРЈ¬AB=2ADЈ¬EОӘұЯABөДЦРөгЈ¬Ҫ«ЎчADEСШЦұПЯDE·ӯЧӘіЙЎчA1DEЈЁA1ЖҪГжABCDЈ©Ј¬ИфMЎўO·ЦұрОӘПЯ¶ОA1CЎўDEөДЦРөгЈ¬ФтФЪЎчADE·ӯЧӘ№эіМЦРЈ¬ПВБРЛө·ЁҙнОуөДКЗЈЁ Ј© 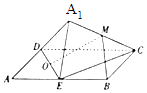
A.УлЖҪГжA1DEҙ№ЦұөДЦұПЯұШУлЦұПЯBMҙ№Цұ
B.ТмГжЦұПЯBMУлA1EЛщіЙҪЗКЗ¶ЁЦө
C.Т»¶ЁҙжФЪДіёцО»ЦГЈ¬К№DEЎНMO
D.ИэАвЧ¶A1©ҒADEНвҪУЗт°лҫ¶УлАвADөДіӨЦ®ұИОӘ¶ЁЦө
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЛ«ЗъПЯ ![]() ©Ғ
©Ғ ![]() =1ЈЁaЈҫ0Ј¬bЈҫ0Ј©өДЧуЎўУТҪ№өг·ЦұрКЗF1 Ј¬ F2 Ј¬ №эF2өДЦұПЯҪ»Л«ЗъПЯөДУТЦ§УЪPЈ¬QБҪөгЈ¬Иф|PF1|=|F1F2|Ј¬ЗТ3|PF2|=2|QF2|Ј¬ФтёГЛ«ЗъПЯөДАлРДВКОӘЈЁ Ј©
=1ЈЁaЈҫ0Ј¬bЈҫ0Ј©өДЧуЎўУТҪ№өг·ЦұрКЗF1 Ј¬ F2 Ј¬ №эF2өДЦұПЯҪ»Л«ЗъПЯөДУТЦ§УЪPЈ¬QБҪөгЈ¬Иф|PF1|=|F1F2|Ј¬ЗТ3|PF2|=2|QF2|Ј¬ФтёГЛ«ЗъПЯөДАлРДВКОӘЈЁ Ј©
A.![]()
B.![]()
C.2
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com