
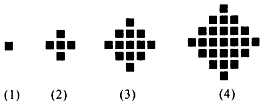
 某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.分析 (1)根据题意,写出f(1)、f(2)、f(3)、f(4)和f(5),f(6)的值;
(2)根据前面5个函数值,得出规律,f(n)-f(n-1)=4(n-1),从而求出f(n)的表达式.
解答 解:(1)根据题意,得出
f(1)=1,f(2)=5,
f(3)=13,f(4)=25,
f(5)=41,f(6)=61;
(2)根据前面四个发现规律:
f(2)-f(1)=4×1,
f(3)-f(2)=4×2,
f(4)-f(3)=4×3,
…,
f(n)-f(n-1)=4(n-1);
这n-1个式子相加可得:f(n)=2n2-2n+1.
点评 本题考查了归纳推理的应用问题,基本思路是先分析,观察,总结其内在联系,得到一般性的结论,是基础题目.


科目:高中数学 来源: 题型:解答题
| 分类 | 患呼吸道疾病 | 未患呼吸道疾病 | 合计 |
| 户外作业人员 | 40 | 60 | 100 |
| 非户外作业人员 | 60 | 240 | 300 |
| 合计 | 100 | 300 | 400 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 0.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (e,+∞) | C. | (-∞,-1) | D. | (-∞,-e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com